Question

【题目】学校为测评班级学生对任课教师的满意度，采用“100分制”打分的方式来计分，规定满意度不低于98分，则评价该教师为“优秀”，现从某班学生中随机抽取10名，以下茎叶图记录了他们对某教师的满意度分数（以十位数字为茎，个位数字为叶）；

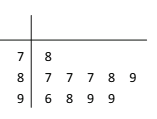
（1）指出这组数据的众数和中位数；

（2）求从这10人中随机选取3人，至多有1人评价该教师是“优秀”的概率；

（3）以这10人的样本数据来估计整个班级的总体数据，若从该班任选3人，记表示抽到评价该教师为“优秀”的人数，求的分布列及数学期望.

Answer 1

【答案】（1）众数：87；中位数：88.5；

（2）；

（3）分布列见解析，

【解析】试题分析：（1）根据茎叶图结合众数与中位数的定义求解；（2）将所求事件分为所选3中无人获得“优秀”与有一个获得“优秀”两种事件，从而利用互斥事件的概率公式求解；（3）首先求得的所有可能取值，然后分别求出相应概率，从而列出分布列，计算出数学期望．

试题解析：（1）由茎叶图知众数为87；中位数＝．

（2）设表示所取3人中有个人评价该教师为“优秀”，至多有1人评价该教师为“优秀”记为事件，则．

（3）的可能取值为0，1，2，3，

； ；

； ；

分布列为

	0	1	2	3

.