题目内容
7.长方体的长、宽、高分别为2、2、2$\sqrt{2}$,则其外接球的表面积为( )| A. | 64π | B. | 32π | C. | 16π | D. | 8π |
分析 长方体的对角线就是外接球的直径,求出长方体的对角线长,即可求出球的半径,再求球的表面积.
解答 解:由题意长方体的对角线就是球的直径,
所以长方体的对角线长为:$\sqrt{4+4+8}$=4,
所以球的直径为:4,半径为:2,
球的表面积是:4πr2=16π.
故选C.
点评 本题是基础题,考查长方体的外接球的半径的求法、球内接多面体、球的体积和表面积,考查计算能力和空间想象能力.

练习册系列答案
相关题目
17.某几何体的三视图如图所示,则俯视图的面积为( )
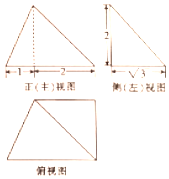

| A. | $5\sqrt{3}$ | B. | $\frac{{5\sqrt{3}}}{2}$ | C. | 5 | D. | $\frac{5}{2}$ |
15.设数列{an}的前n项和为Sn,对任意n∈N*,函数f(x)=x2-Sncosx+2an-n在定义域内有唯一的零点.若不等式$\frac{λ}{n}$≥$\frac{n+1}{{a}_{n}+1}$对任意n∈N*恒成立,则实数λ的最小值是( )
| A. | 1 | B. | $\frac{5}{4}$ | C. | $\frac{3}{2}$ | D. | 2 |
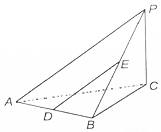 如图,在三棱锥P-ABC中,PC⊥底面ABC,△ABC为等腰直角三角形,∠ABC=90°,D,E分别是AB,PB的中点.
如图,在三棱锥P-ABC中,PC⊥底面ABC,△ABC为等腰直角三角形,∠ABC=90°,D,E分别是AB,PB的中点.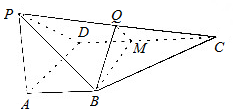 四棱锥P-ABCD中,PA⊥底面ABCDD,且PA=AB=AD=$\frac{1}{2}$CD,AB∥CD,∠ADC=90°,M是CD上的点,Q点是PC上的点,平面BMQ∥平面PAD.
四棱锥P-ABCD中,PA⊥底面ABCDD,且PA=AB=AD=$\frac{1}{2}$CD,AB∥CD,∠ADC=90°,M是CD上的点,Q点是PC上的点,平面BMQ∥平面PAD.