题目内容
已知空间四边形OABC中，OA=OB，CA=CB，E、F、G、H分别为OA、OB、BC、CA的中点，求证：四边形EFGH是矩形．
证明：∵E、F、G、H分别是OA、OB、BC、CA的中点，
∴
，
，
=
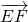，∴EFGH是平行四边形．
．
∵OA=OB，CA=CB（已知），OC=OC，∴△BOC≌△AOC．∴∠BOC=∠AOC．
∴
，∴
，∴
，
∴四边形EFGH是矩形．
分析：利用向量证明EFGH是平行四边形，化简
的解析式，由△BOC≌△AOC，可得∠BOC=∠AOC，，从而得到=0，从而得到四边形EFGH是矩形．
点评：本题主要考查两个向量的数乘运算及其几何意义，两个向量共线的条件，属于基础题．
∴
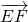，，=，∴EFGH是平行四边形．．∵OA=OB，CA=CB（已知），OC=OC，∴△BOC≌△AOC．∴∠BOC=∠AOC．
∴
，∴，∴，∴四边形EFGH是矩形．
分析：利用向量证明EFGH是平行四边形，化简
的解析式，由△BOC≌△AOC，可得∠BOC=∠AOC，，从而得到=0，从而得到四边形EFGH是矩形．点评：本题主要考查两个向量的数乘运算及其几何意义，两个向量共线的条件，属于基础题．
练习册系列答案
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案
相关题目
，可构成空间向量的一组基底，若
，
，
，在向量已有的运算法则基础上，新定义一种运算
．显然a×b的结果仍为一向量，记作p．
平移，得到一个平行六面体
，试判断平行六面体的体积V与|(a×b)·c|的大小．
，可构成空间向量的一组基底，若
，在向量已有的运算法则基础上，新定义一种运算
．显然
的结果仍为一向量．
；
平移，得到一个平行六面体
，试判断平行六面体的体积V与
的大小关系．
