题目内容
如图,已知抛物线C:y2=4x的焦点为F,过F的直线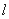 与抛物线C交于A(x1,y1)(y1>0),B(x2,y2)两点,T为抛物线的准线与x轴的交点.
与抛物线C交于A(x1,y1)(y1>0),B(x2,y2)两点,T为抛物线的准线与x轴的交点.
(1)若 ,求直线
,求直线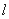 的斜率.
的斜率.
(2)求∠ATF的最大值.
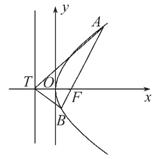
解:(1)因为抛物线y2=4x焦点为F(1,0),T(-1,0).
当 轴时,A(1,2),B(1,-2),此时
轴时,A(1,2),B(1,-2),此时 ,与
,与 矛盾…2分
矛盾…2分
所以设直线 的方程为y=k(x-1),
的方程为y=k(x-1),
代入y2=4x,得k2x2-(2k2+4)x+k2=0,
则 ,①
,①
所以 ,所以y1y2=-4, ②
,所以y1y2=-4, ②
因为 ,所以(x1+1)(x2+1)+y1y2=1,
,所以(x1+1)(x2+1)+y1y2=1,
将①②代入并整理得,k2=4,所以k=±2.……………6分
(2)因为y1>0,
所以,
当且仅当 ,即y1=2时,取等号,
,即y1=2时,取等号,
所以∠ATF≤ ,所以∠ATF的最大值为
,所以∠ATF的最大值为 .……………12分
.……………12分

练习册系列答案
相关题目
 ,
, ,
, ,则( )
,则( ) B
B  C
C  D
D 
 的一个焦点为(0,3), 则实数
的一个焦点为(0,3), 则实数 的值为 .
的值为 . 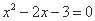 ,则
,则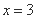 ”的逆否命题为:“若
”的逆否命题为:“若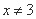 ,则
,则 ”;
”; 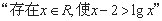 的否定是
的否定是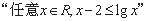 ;
; 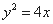 上”是“点M的坐标满足方程
上”是“点M的坐标满足方程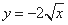 ”的必要不充分条件;
”的必要不充分条件; 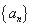 是等比数列,则“
是等比数列,则“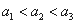 ”是“数列
”是“数列
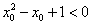 ”;
”; + a 对应的直线一定经过其样本数据点( x 1 , y1)、( x2 , y2)、…,
+ a 对应的直线一定经过其样本数据点( x 1 , y1)、( x2 , y2)、…, 下结论中:
下结论中: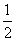 a .
a . ( )
( ) 中,已知角
中,已知角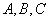 所对的边分别为
所对的边分别为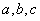 ,已知
,已知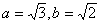 ,
,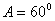 ,则角
,则角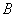 =( )
=( ) A
A 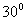 B
B 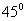 C
C 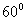 D
D