题目内容
(05年北京卷理)(14分)
如图,在直四棱柱![]() 中,
中,![]() ,
,
![]() 垂足为
垂足为![]()
![]()
(Ⅰ)求证![]() ;
;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)求异面直线![]() 与
与![]() 所成角的大小
所成角的大小![]()

解析:(I)在直四棱柱ABCD-AB1C1D1中,
∵AA1⊥底面ABCD.∴ AC是A1C在平面ABCD上的射影.
∵BD⊥AC.∴ BD⊥A1C;
(II)连结A1E,C1E,A1 C1.
与(I)同理可证BD⊥A1E,BD⊥C1E,
∴ ∠A1EC1为二面角A1-BD-C1的平面角.
∵ AD⊥DC,∴ ∠A1D1C1=∠ADC=90°,
又A1D1=AD=2,D1C1= DC=2![]() ,AA1=
,AA1=![]() 且 AC⊥BD,
且 AC⊥BD,
∴ A1C1=4,AE=1,EC=3,∴ A1E=2,C1E=2![]() ,
,
在△A1EC1中,A1C12=A1E2+C1E2, ∴ ∠A1EC1=90°,
即二面角A1-BD-C1的大小为90°.
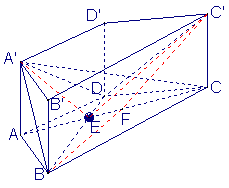
(III)过B作 BF//AD交 AC于 F,连结FC1,
则∠C1BF就是AD与BC1所成的角.
∵ AB=AD=2, BD⊥AC,AE=1,
∴ BF=2,EF=1,FC=2,BC=DC,∴ FC1=![]() ,BC1=
,BC1=![]() ,
,
在△BFC1 中,![]() ,∴ ∠C1BF=
,∴ ∠C1BF=![]()
即异面直线AD与BC1所成角的大小为![]() .
.
解法二:
(Ⅰ)同解法一![]()
(Ⅱ)如图,以D为坐标原点,![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]()
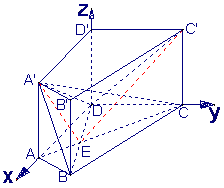
连结![]()
与(1)同理可证,![]() ,
,
∴![]() 为二面角
为二面角![]() 的平面角.
的平面角.
由![]()
得![]()
![]()
∴![]()
∴![]() 即
即![]()
∴二面角![]() 的大小为
的大小为![]()
(Ⅲ)如图,由![]() ,
,![]()
![]()
得![]()
∴![]()
∴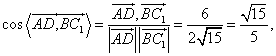
∵异面直线![]() 与
与![]() 所成角的大小为
所成角的大小为![]()
![]()
解法三:
(Ⅰ)同解法一.
(Ⅱ)如图,建立空间直角坐标系,坐标原点为E.连结![]() .
.

与(Ⅰ)同理可证![]()
∴![]() 为二面角
为二面角![]() 的平面角
的平面角![]()
由![]()
得![]()
∵![]()
∴![]() 即
即![]()
∴二面角![]() 的大小为
的大小为![]()
![]()

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目