题目内容
在△ABC中,三边对应的向量满足(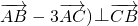
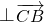 ,则角A的最大值为________.
,则角A的最大值为________.

分析:由题意可得
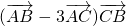 =0,化简得ac•cosB-3ab•cos(π-C)=0,再利用正弦定理求得tanC=-3tanB,判断A为锐角,故 tanA>0,利用基本不等式求得tanA≤
=0,化简得ac•cosB-3ab•cos(π-C)=0,再利用正弦定理求得tanC=-3tanB,判断A为锐角,故 tanA>0,利用基本不等式求得tanA≤ ,由此求得A的最大值.
,由此求得A的最大值.解答:在△ABC中,(
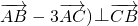
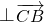 ,∴
,∴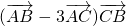 =0.
=0.即
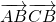 -3
-3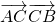 =0,即ac•cosB-3ab•cos(π-C)=0.
=0,即ac•cosB-3ab•cos(π-C)=0.化简可得
 =-
=-
 ,∴
,∴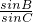 =-
=-
 ,解得tanC=-3tanB,
,解得tanC=-3tanB,故tanC与tanB符号相反,故 B或C中有一个为钝角,故A为锐角,故 tanA>0.
∴tanA=-tan(B+C)=
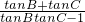 =
=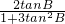 =
=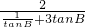 >0,
>0,故有tanB>0,再由基本不等式可得
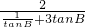 ≤
≤ ,即tanA≤
,即tanA≤ ,故A的最大值为
,故A的最大值为 ,
,故答案为
 .
.点评:本题主要考查两个向量垂直的性质,两个向量的数量积的定义,正弦定理以及基本不等式的应用,属于中档题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目