题目内容
已知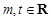 ,函数
,函数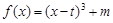 .
.
(Ⅰ)当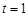 时,
时,
(1)若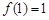 ,求函数
,求函数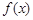 的单调区间;
的单调区间;
(2)若关于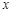 的不等式
的不等式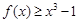 在区间
在区间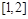 上有解,求
上有解,求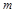 的取值范围;
的取值范围;
(Ⅱ)已知曲线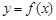 在其图象上的两点
在其图象上的两点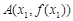 ,
,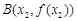 (
(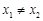 )处的切线分别为
)处的切线分别为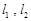 .若直线
.若直线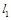 与
与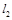 平行,试探究点
平行,试探究点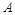 与点
与点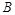 的关系,并证明你的结论.
的关系,并证明你的结论.
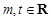 ,函数
,函数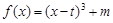 .
.(Ⅰ)当
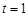 时,
时,(1)若
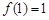 ,求函数
,求函数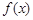 的单调区间;
的单调区间;(2)若关于
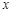 的不等式
的不等式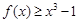 在区间
在区间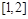 上有解,求
上有解,求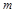 的取值范围;
的取值范围;(Ⅱ)已知曲线
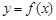 在其图象上的两点
在其图象上的两点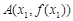 ,
,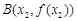 (
(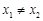 )处的切线分别为
)处的切线分别为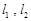 .若直线
.若直线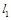 与
与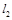 平行,试探究点
平行,试探究点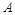 与点
与点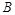 的关系,并证明你的结论.
的关系,并证明你的结论.(Ⅰ)(1) 单调递增区间为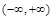 ;(2)
;(2) 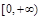 ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
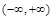 ;(2)
;(2) 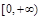 ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.试题分析:(Ⅰ)(1)根据
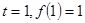 求出
求出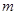 的值,然后利用
的值,然后利用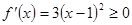 ,得到函数在定义域内都是单调递增的,从而写出其单调区间;
,得到函数在定义域内都是单调递增的,从而写出其单调区间;(2)当
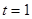 时,将不等式化简,整理为
时,将不等式化简,整理为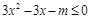 在区间
在区间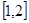 上有解问题,可以反解
上有解问题,可以反解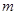 ,利用不等式
,利用不等式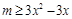 在区间
在区间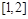 上有解,即
上有解,即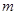 大于等于其最小值,转化为求
大于等于其最小值,转化为求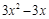 在区间
在区间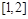 上的最小值,
上的最小值,(Ⅱ)
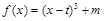 的对称中心为
的对称中心为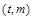 ,故合情猜测,若直线
,故合情猜测,若直线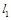 与
与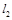 平行,则点
平行,则点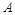 与点
与点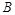 关于点
关于点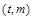 对称.然后对猜测进行证明,首先求其两点处的导数,即两切线的斜率,利用平行及斜率相等,证明
对称.然后对猜测进行证明,首先求其两点处的导数,即两切线的斜率,利用平行及斜率相等,证明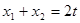 ,
, .
.试题解析:(Ⅰ)(1)因为
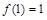 ,所以
,所以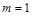 , 1分
, 1分则
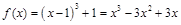 ,
,而
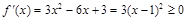 恒成立,
恒成立,所以函数
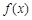 的单调递增区间为
的单调递增区间为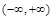 . 4分
. 4分(2)不等式
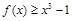 在区间
在区间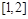 上有解,
上有解,即不等式
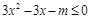 在区间
在区间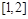 上有解,
上有解,即不等式
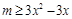 在区间
在区间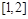 上有解,
上有解,等价于
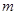 不小于
不小于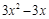 在区间
在区间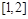 上的最小值. 6分
上的最小值. 6分因为
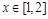 时,
时,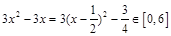 ,
,所以
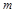 的取值范围是
的取值范围是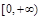 . 9分
. 9分Ⅱ.因为
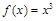 的对称中心为
的对称中心为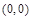 ,
,而
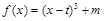 可以由
可以由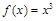 经平移得到,
经平移得到,所以
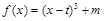 的对称中心为
的对称中心为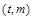 ,故合情猜测,若直线
,故合情猜测,若直线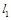 与
与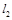 平行,
平行,则点
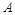 与点
与点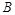 关于点
关于点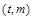 对称. 10分
对称. 10分对猜想证明如下:
因为
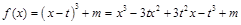 ,
,所以
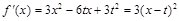 ,
,所以
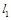 ,
,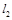 的斜率分别为
的斜率分别为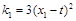 ,
,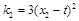 .
.又直线
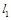 与
与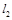 平行,所以
平行,所以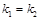 ,即
,即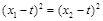 ,
,因为
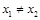 ,所以,
,所以,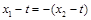 , 12分
, 12分从而
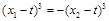 ,
,所以
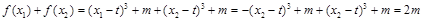 .
.又由上
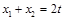 ,
,所以点
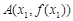 ,
,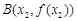 (
(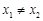 )关于点
)关于点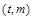 对称.
对称.故当直线
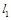 与
与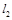 平行时,点
平行时,点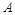 与点
与点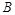 关于点
关于点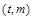 对称. 14分
对称. 14分
练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 元(
元( )时,一年的销售量为
)时,一年的销售量为 万件。
万件。 .
. 的单调性;
的单调性;  ,求
,求 上的最大值;
上的最大值; ,不等式
,不等式 都成立(其中
都成立(其中 是自然对数的底数).
是自然对数的底数). ,
, .
. 在其定义域上为增函数,求
在其定义域上为增函数,求 的取值范围;
的取值范围; 时,函数
时,函数 在区间
在区间 上存在极值,求
上存在极值,求 的最大值.
的最大值. ≈
≈ ).
).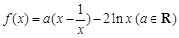 .
.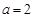 ,求曲线
,求曲线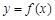 在点
在点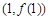 处的切线方程;
处的切线方程;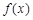 的单调区间;
的单调区间;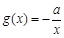 .若至少存在一个
.若至少存在一个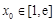 ,使得
,使得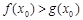 成立,求实数
成立,求实数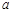 的取值范围.
的取值范围.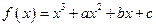 有极值点
有极值点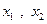 ,且
,且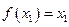 ,则关于x的方程
,则关于x的方程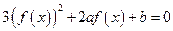 的不同实根个数是( )
的不同实根个数是( )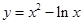 上任意一点,则点P到直线
上任意一点,则点P到直线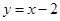 的距离的最小值是
的距离的最小值是  在
在 内有定义,对于给定的正数
内有定义,对于给定的正数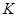 ,定义函数
,定义函数 ,取函数
,取函数 ,恒有
,恒有 ,则( )
,则( )