题目内容
已知命题p：∀x1，x2∈R，(f(x2)－f(x1))(x2－x1)≥0，则綈p是 ( )
A．∃x1，x2∈R，(f(x2)－f(x1))(x2－x1)≤0
B．∀x1，x2∈R，(f(x2)－f(x1))(x2－x1)≤0
C．∃x1，x2∈R，(f(x2)－f(x1))(x2－x1)<0
D
．∀x1，x2∈R，(f(x2)－f(x1))(x2－x1)<0
C
分析 首先确定已知命题中所含的量词，然后根据含有一个量词的命题的否定形式进行判断即可．
解析 已知命题是一个全称命题，由全称命题的否定形式，可知其否定是一个特称命题，把全称量词“∀”改为存在量词“∃”，然后把“(f(x2)－f(x1))(x2－x1)≥0”改为“(f(x2)－f(x1))(x2－x1)<0”，即可得到该命题的否定形式为“∃x1，x2∈R，(f(x2)－f(x1))(x2－x1)<0”，故选C.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
恒成立，命题q：∃x∈R，使x2＋ax＋2＜0，若p是真命题，q是假命题，求a的取值范围．
，
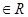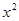>0，则（
）
B．非p：∀x
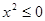
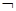p：∃x0∈R，sin
x0≥1