题目内容
11.下列函数中,满足“f(x+y)=f(x)f(y)”的单调递减函数是( )| A. | f(x)=x${\;}^{\frac{1}{2}}$ | B. | f(x)=x3 | C. | f(x)=($\frac{1}{2}$)x | D. | f(x)=3x |
分析 根据指数函数图象和性质,得到C单调递减,D单调递增,根据幂函数图象和性质得到A,B均为单调递增,再验证C是否满足f(x+y)=f(x)f(y).
解答 解:根据指数函数图象和性质,得到C单调递减,D单调递增,
根据幂函数图象和性质得到A,B均为单调递增,
对于C,f(x+y)=$(\frac{1}{2})^{x+y}$=$(\frac{1}{2})^{x}$•$(\frac{1}{2})^{y}$=f(x)f(y),
故C符合,
故选:C
点评 本题考查了指数函数和幂函数的图象和性质,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.如函数f(x)=$\sqrt{2}$sin(ax+$\frac{π}{4}$)(a>0)的最小正周期为1,且g(x)=$\left\{\begin{array}{l}{sinax(x<0)}\\{g(x-1)(x≥0)}\end{array}\right.$,则g($\frac{5}{6}$)等于( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
19.执行如图所示的程序框图,则输出的S的值为( )


| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
1.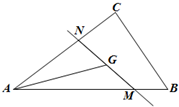 如图,直线MN过△ABC的重心G(重心是三角形三条中线的交点),设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,且$\overrightarrow{AM}$=m$\overrightarrow{a}$,$\overrightarrow{AN}$=n$\overrightarrow{b}$(其中m>0,n>0),则mn的最小值是( )
如图,直线MN过△ABC的重心G(重心是三角形三条中线的交点),设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,且$\overrightarrow{AM}$=m$\overrightarrow{a}$,$\overrightarrow{AN}$=n$\overrightarrow{b}$(其中m>0,n>0),则mn的最小值是( )
 如图,直线MN过△ABC的重心G(重心是三角形三条中线的交点),设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,且$\overrightarrow{AM}$=m$\overrightarrow{a}$,$\overrightarrow{AN}$=n$\overrightarrow{b}$(其中m>0,n>0),则mn的最小值是( )
如图,直线MN过△ABC的重心G(重心是三角形三条中线的交点),设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,且$\overrightarrow{AM}$=m$\overrightarrow{a}$,$\overrightarrow{AN}$=n$\overrightarrow{b}$(其中m>0,n>0),则mn的最小值是( )| A. | $\frac{2}{9}$ | B. | $\frac{1}{2}$ | C. | $\frac{4}{9}$ | D. | $\frac{2}{3}$ |