题目内容

已知f(x)=,Pn(an,)在曲线y=f(x)上(n∈N+)且a1=1,an＞0.

(1)求{an}的通项公式.

(2)数列{bn}的前n项和为Tn,且满足+16n2-8n-3.设定b1的值,使得数列{bn}是等差数列.

解:(1)由已知Pn在曲线y=f(x)上,

∴=.

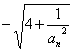∴=4.

∴{}是等差数列,

=1+4(n-1)=4n-3.

∵an＞0,∴an=.

(2)∵=+16n2-8n-3=+(4n-3)(4n+1),

即(4n-3)Tn+1=(4n+1)Tn+(4n-3)(4n+1),

∴=+1.

∴{}为等差数列,首项为=b1,=b1+(n-1)=n+(b1-1).

∴Tn=(4n-3)［n+(b1-1)］=4n2+(4b1-7)n-3(b1-1).

要使{bn}为等差数列,需使b1-1=0,∴b1=1.

当b1=1时,Tn=4n2-3n,bn=8n-7.

∴{bn}为等差数列.

练习册系列答案
相关题目
已知f(x)=
4+
1
x2
，数列{an}的前n项和为Sn，点Pn（an，
1
an+1
）（n∈N*）在曲线y=f（x）上，且a1=1，an＞0．
（1）求数列{an}的通项公式an；
（2）数列{bn}的首项b1=1，前n项和为Tn，且
Tn+1
an2
=
Tn
an+12
+16n2-8n-3，求数列{bn}的通项公式bn．
（2013•乐山二模）已知f(x)=-
4+
1
x2
，点Pn(an，-
1
an+1
)在曲线y=f（x）上（n∈N*）且a1=1，an＞0．
（Ⅰ）求证：数列{
1
a
2
n
}为等差数列，并求数列{an}的通项公式；
（Ⅱ）设数列{
a
2
n
•
a
2
n+1
}的前n项和为Sn，若对于任意的n∈N*，存在正整数t，使得Sn＜t2-t-
1
2
恒成立，求最小正整数t的值．
已知f(x)=-
4+
1
x2
，数列{an}的前n项和为Sn，点Pn(an，-
1
an+1
)在曲线y=f（x）上（n∈N*），且a1=1，an＞0．
（1）求数列{an}的通项公式；
（2）数列{bn]的前n项和为Tn，且满足
Tn+1
an2
=
Tn
an+12
+16n2-8n-3，b1=1，求证：数列{
Tn
4n-3
}是等差数列，并求数列{bn]的通项公式．
已知f(x)=,Pn(an,)在曲线y=f(x)上(n∈N+)且a1=1,an＞0.

(1)求{an}的通项公式.

(2)数列{bn}的前n项和为Tn,且满足+16n2-8n-3.设定b1的值,使得数列{bn}是等差数列.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网