题目内容
若三条直线l1：4x+y=4，l2：mx+y=0，l3：2x-3my=4：能围成三角形，求m的取值范围。
解：问题转化为三条直线交于一点或至少有两条直线平行或重合，
（Ⅰ）三线交于一点解方程组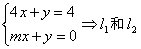
的交点A的坐标
，
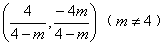若A在l3上，则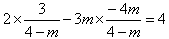
，解得
；
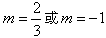（Ⅱ）若l1与l2平行（或重合），则易知m=4；
若l1与l3平行（或重合），则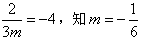
；
若l2与l3平行（或重合），则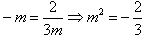
无解；
综上，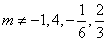
。
（Ⅰ）三线交于一点解方程组
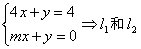的交点A的坐标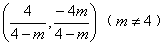，若A在l3上，则
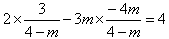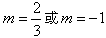，解得；（Ⅱ）若l1与l2平行（或重合），则易知m=4；
若l1与l3平行（或重合），则
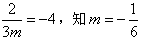；若l2与l3平行（或重合），则
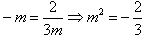无解； 综上，
。 
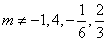练习册系列答案
相关题目
已知三条直线l1：4x+y=1，l2：x-y=0，l3：2x-my=3，若l1关于l2的对称直线与l3垂直，则实数m的值是（ ）
| A、-8 | ||
B、-
| ||
| C、8 | ||
D、
|
