Question

如图所示,直线AC和DF被三个平行平面α、β、γ所截,已知直线AC与α相交成60°角,BA=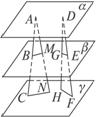4 cm,BC=12 cm,DF=10 cm,求:

(1)平面α与平面γ的距离;

(2)DE和EF的长.

Answer 1

解析:(1)设A在平面β上的射影为M,

∴AM⊥β.

又∵β∥γ,

∴AM⊥γ.设垂足为N,则AN的长为α和γ间的距离.

∵AC与α所成角为60°,α∥γ,

∴AC与γ所成的角也为60°,

即∠ACN=60°.

在Rt△ANC中,AN=AC sin∠ACN=(4+12)·sin60°=(cm).

(2)过点D作DH⊥γ,垂足为H,交β于G,则DH⊥β.

∵AN⊥γ,

∴AN=DH,AM=DG.

又由两干面平行的性质定理得BM∥CN,GE∥HF,

∴.

∴.

∴DE=×10=2.5(cm).

∴EF=DF-DE=10-2.5=7.5(cm).