题目内容
选做题:(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)A.(选修4-4坐标系与参数方程)已知点A是曲线ρ=2sinθ上任意一点,则点A到直线
 的距离的最小值是 .
的距离的最小值是 .B.(选修4-5不等式选讲)不等式|2x-1|+|2x-3|≥4的解集是 .
C.(选修4-1几何证明选讲)如图所示,AC和AB分别是圆O的切线,且OC=3,AB=4,延长AO到D点,则△ABD的面积是 .

【答案】分析:A 曲线方程化为直角坐标方程为 x2+(y-1)2=1,表示以(0,1)为圆心,以1为半径的圆,把直线方程化为直角坐标方程,求出圆心到直线的距离 d,d-1即为所求.
B 把不等式转化为与之等价的三个不等式组,解出每个不等式组的解集,取并集即为所求.
C 令∠AOB=θ,则∠BOD=π-θ. Rt△AOB中,由勾股定理可得 AO,由正弦定理求得sinθ的值,根据△ABD的面积 S△ABD=S△ABO+S△BOD,运算求得结果.
解答:解:A 曲线ρ=2sinθ即 ρ2=2ρsinθ,化为直角坐标方程为 x2+(y-1)2=1,表示以(0,1)为圆心,以1为半径的圆.
直线 即
即  +
+ =4,化为直角坐标方程为
=4,化为直角坐标方程为  .
.
由于圆心到直线的距离等于 d= =
= ,
,
故点A到直线 的距离的最小值为
的距离的最小值为  -1=
-1= .
.
故答案为 .
.
B 由不等式|2x-1|+|2x-3|≥4 可得 ①,或
①,或  ②,或
②,或  ③.
③.
解①得 x≤0,解②得 x∈∅,解 ③得 x≥2.
故原不等式的解集为{x|x≤0,或 x≥2},
故答案为 (-∞,0]∪[2,+∞).
C 令∠AOB=θ,则∠BOD=π-θ. Rt△AOB中,由勾股定理可得 AO= =
= =5.
=5.
由正弦定理可得 ,即
,即  ,∴sinθ=
,∴sinθ= .
.
故△ABD的面积 S△ABD=S△ABO+S△BOD= +
+ =
= +
+ =
= .
.
故答案为 .
.
点评:本题主要考查把极坐标方程化为直角坐标方程的方法,绝对值不等式的解法,圆的切线性质定理的应用,属于中档题.
B 把不等式转化为与之等价的三个不等式组,解出每个不等式组的解集,取并集即为所求.
C 令∠AOB=θ,则∠BOD=π-θ. Rt△AOB中,由勾股定理可得 AO,由正弦定理求得sinθ的值,根据△ABD的面积 S△ABD=S△ABO+S△BOD,运算求得结果.
解答:解:A 曲线ρ=2sinθ即 ρ2=2ρsinθ,化为直角坐标方程为 x2+(y-1)2=1,表示以(0,1)为圆心,以1为半径的圆.
直线
 即
即  +
+ =4,化为直角坐标方程为
=4,化为直角坐标方程为  .
.由于圆心到直线的距离等于 d=
 =
= ,
,故点A到直线
 的距离的最小值为
的距离的最小值为  -1=
-1= .
.故答案为
 .
.B 由不等式|2x-1|+|2x-3|≥4 可得
 ①,或
①,或  ②,或
②,或  ③.
③.解①得 x≤0,解②得 x∈∅,解 ③得 x≥2.
故原不等式的解集为{x|x≤0,或 x≥2},
故答案为 (-∞,0]∪[2,+∞).
C 令∠AOB=θ,则∠BOD=π-θ. Rt△AOB中,由勾股定理可得 AO=
 =
= =5.
=5.由正弦定理可得
 ,即
,即  ,∴sinθ=
,∴sinθ= .
.故△ABD的面积 S△ABD=S△ABO+S△BOD=
 +
+ =
= +
+ =
= .
.故答案为
 .
.点评:本题主要考查把极坐标方程化为直角坐标方程的方法,绝对值不等式的解法,圆的切线性质定理的应用,属于中档题.

练习册系列答案
相关题目
 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)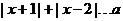 对任意
对任意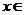 R恒成立,则
R恒成立,则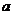 的取值范围是
.
的取值范围是
.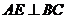 ,
, ,且AB=6,AC=4,AD=12,则AE= .
,且AB=6,AC=4,AD=12,则AE= .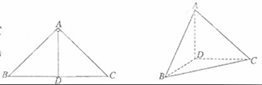
 中,以原点O为极点,
中,以原点O为极点,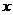 轴的正半轴为极轴建立极坐标系,设点A,B分别在曲线
轴的正半轴为极轴建立极坐标系,设点A,B分别在曲线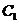 :
: (
(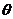 为参数)和曲线
为参数)和曲线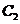 :
: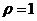 上,则
上,则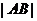 的最小值为
.
的最小值为
. 的不等式
的不等式 存在实数解,则实数
存在实数解,则实数 的取值范围是
.
的取值范围是
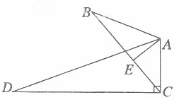
. B.(几何证明选做题)如图,∠B=∠D,
B.(几何证明选做题)如图,∠B=∠D, ,
, ,且AB=6,AC=4,AD=12,则BE= .
,且AB=6,AC=4,AD=12,则BE= . 中,以原点O为极点,
中,以原点O为极点, :
: (
( 为参数)和曲线
为参数)和曲线 :
: 上,则
上,则 的最小值为
.
的最小值为
. A.(不等式选做题)若关于
A.(不等式选做题)若关于