题目内容
在各项均为正数的等比数列{an}中,已知a2=2a1+3,且3a2,a4,5a3成等差数列.
(1) 求数列{an}的通项公式;
(2) 设bn=log3an,求数列{anbn}的前n项和Sn.
解:(1) 设{an}公比为q,由题意得q>0,
且
解得 (舍),
(舍),
所以数列{an}的通项公式为an=3·3n-1=3n,n∈N.
(2) 由(1)可得bn=log3an=n,所以anbn=n·3n.
所以Sn=1·3+2·32+3·33+…+n·3n,
所以3Sn=1·32+2·33+3·34+…+n·3n+1,
两式相减得,2Sn=-3-(32+33+…+3n)+n·3n+1=-(3+32+33+…+3n)+n·3n+1
=- +n·3n+1=
+n·3n+1= ,
,
所以数列{anbn}的前n项和Sn= .
.

练习册系列答案
相关题目
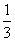 ,0,
,0,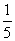 ,0,
,0,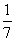 ,…
,… …
…
 ,且A、B、C三点共线(该直线不过点O),则S200=________.
,且A、B、C三点共线(该直线不过点O),则S200=________.