题目内容
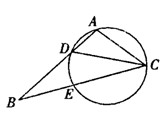
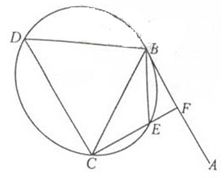
如图,在 中,
中,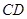 是
是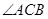 的角平分线,
的角平分线,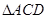 的外接圆交
的外接圆交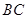 于
于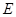 ,
,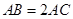 .
.
(1)求证: ;
;
(2)当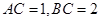 时,求
时,求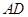 的长.
的长.
(1)证明过程详见解析;(2) .
.
解析试题分析:本题主要以圆为几何背景考查线线相等的证明及相似三角形的证明,考查学生的转化能力和化归能力.第一问,运用相似三角形的基本方法求证;第二问,借助割线定理证明相等关系,列出表达式,通过解方程求边长.
试题解析: (1)连结 ,
,
∵ 为圆的内接四边形,∴
为圆的内接四边形,∴ ,又
,又 ,
,
∴ ,即
,即 ,而
,而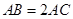 ,∴
,∴ .
.
又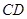 是
是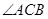 的平分线,∴
的平分线,∴ ,从而
,从而 .(5分)
.(5分)
(2)由条件得 ,设
,设 .
.
根据割线定理得 ,即
,即 ,∴
,∴ ,
,
解得 ,即
,即 .(10分)
.(10分)
考点:1.相似三角形的判定和性质;2.割线定理.

练习册系列答案
相关题目

 ,AF=3,求FG的长.
,AF=3,求FG的长.
 =
= ,求
,求 的值.
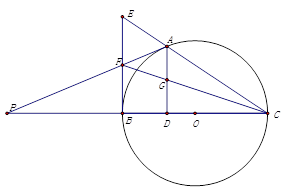
的值. 是以线段
是以线段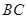 为直径的圆
为直径的圆 上一点,
上一点,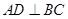 于点
于点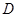 ,过点
,过点 作圆
作圆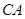 的延长线交于点
的延长线交于点 ,点
,点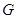 是
是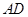 的中点,连结
的中点,连结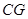 并延长与
并延长与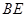 相交于点
相交于点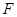 ,延长
,延长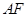 与
与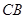 的延长线相交于点
的延长线相交于点 .
.
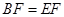 ;
;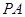 是圆
是圆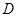 为
为 的
的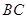 边上一点,
边上一点,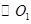 经过点
经过点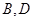 ,交
,交 于另一点
于另一点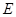 ,
,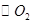 经过点
经过点 ,
,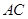 于另一点
于另一点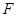 ,
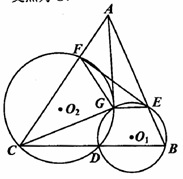
,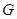 .
.
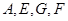 四点共圆;
四点共圆;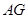 切
切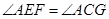 .
.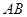 为圆的切线,切点为
为圆的切线,切点为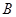 ,点
,点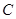 在圆上,
在圆上, 的角平分线
的角平分线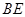 交圆于点
交圆于点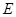 ,
,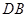 垂直
垂直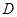 。
。
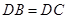 ;
; ,
,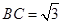 ,延长
,延长 交
交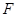 ,求
,求 外接圆的半径。
外接圆的半径。 切⊙
切⊙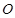 于点E,割线PBA交⊙
于点E,割线PBA交⊙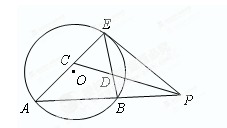
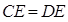 ; (Ⅱ)
; (Ⅱ)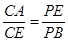 .
.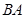 是圆
是圆 的直径,
的直径, 、
、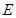 在圆
在圆 、
、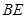 的延长线交直线
的延长线交直线 于点
于点 、
、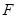 ,
,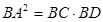 求证:
求证: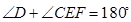
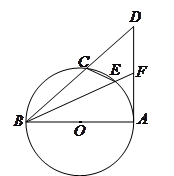

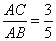 ,求
,求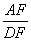 的值.
的值.