题目内容
直四棱柱ABCD-A1B1C1D1中,∠ADC=90°,△ABC为等边三角形,且AA1=AD=DC=2,
(Ⅰ)求异面直线AC1与BC所成的角余弦值;
(Ⅱ)求证:BD⊥平面AC1;
(Ⅲ)求二面角B-AC1-C的正切值。
(Ⅰ)求异面直线AC1与BC所成的角余弦值;
(Ⅱ)求证:BD⊥平面AC1;
(Ⅲ)求二面角B-AC1-C的正切值。

解:(Ⅰ)在直四棱柱ABCD-A1B1C1D1中,BC∥B1C1,
∠AC1B1是异面直线AC1与BC所成的角,
在△AC1B1中,AC1=AB1= ,C1B1=
,C1B1= ,cos∠AC1B1=
,cos∠AC1B1= ,
,
故异面直线AC1与BC所成的角的余弦值为 ;
;
(Ⅱ)因为AD=DC,AB=BC,可得BD⊥AC(垂直平分线),
又CC1⊥平面ABCD,AC为AC1平面ABCD上的射影,
所以BD⊥平面AC1;
(Ⅲ)设AC∩BD=O,
由(Ⅱ)得BD⊥平面ACC1,
过O作OH⊥AC1,垂足为H,连接BH,则BH⊥AC1,
∠OHB为二面角B-AC1-C的平面角,
在Rt△OBH中,OB= ,OH=
,OH=
 tan∠OHB=3,
tan∠OHB=3,
故二面角B-AC1-C的正切值为3。
∠AC1B1是异面直线AC1与BC所成的角,
在△AC1B1中,AC1=AB1=
 ,C1B1=
,C1B1= ,cos∠AC1B1=
,cos∠AC1B1= ,
,故异面直线AC1与BC所成的角的余弦值为
 ;
;(Ⅱ)因为AD=DC,AB=BC,可得BD⊥AC(垂直平分线),
又CC1⊥平面ABCD,AC为AC1平面ABCD上的射影,
所以BD⊥平面AC1;
(Ⅲ)设AC∩BD=O,
由(Ⅱ)得BD⊥平面ACC1,
过O作OH⊥AC1,垂足为H,连接BH,则BH⊥AC1,
∠OHB为二面角B-AC1-C的平面角,
在Rt△OBH中,OB=
 ,OH=
,OH=
 tan∠OHB=3,
tan∠OHB=3,故二面角B-AC1-C的正切值为3。

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
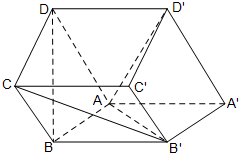 如图,在直四棱柱ABCD-A′B′C′D′中,底面ABCD为梯形,BC∥AD,AA′=AB=
如图,在直四棱柱ABCD-A′B′C′D′中,底面ABCD为梯形,BC∥AD,AA′=AB=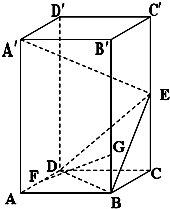 已知直四棱柱ABCD-A′B′C′D′,四边形ABCD为正方形,AA′=2AB=2,E为棱CC′的中点.
已知直四棱柱ABCD-A′B′C′D′,四边形ABCD为正方形,AA′=2AB=2,E为棱CC′的中点.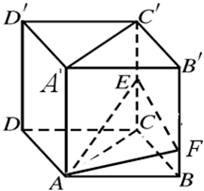 已知直四棱柱ABCD-A′B′C′D′的底面是菱形,∠ABC=60°,E、F分别是棱CC′与BB′上的点,且EC=BC=2FB=2.
已知直四棱柱ABCD-A′B′C′D′的底面是菱形,∠ABC=60°,E、F分别是棱CC′与BB′上的点,且EC=BC=2FB=2.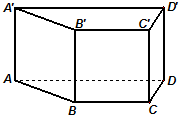 在高为1的直四棱柱ABCD-A'B'C'D'中,底面ABCD是等腰梯形,AB=BC=CD=1,AD=2.
在高为1的直四棱柱ABCD-A'B'C'D'中,底面ABCD是等腰梯形,AB=BC=CD=1,AD=2. 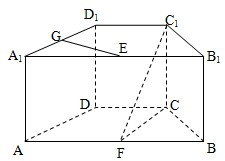 (2009•崇明县一模)如图,在直四棱柱ABCD-A'B'C'D'中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E、F、G分别是棱A1B1、AB、A1D1的中点.
(2009•崇明县一模)如图,在直四棱柱ABCD-A'B'C'D'中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E、F、G分别是棱A1B1、AB、A1D1的中点.