题目内容
【题目】如图所示,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD是梯形,AB//CD,DA⊥AB,BC⊥SC,SA=AD=3,AB=6,点E在棱SD上,且VS-ACE=2VE-ACD。

(1)求证:BC⊥平面SAC;
(2)求二面角S-AE-C的余弦值。
【答案】(1)详见解析;(2)![]()
【解析】
(1)由![]() 平面
平面![]() 得到
得到![]() ,结合
,结合![]() ,得到
,得到![]() 平面
平面![]() .(2)以
.(2)以![]() 为坐标原点建立空间直角坐标系,通过平面
为坐标原点建立空间直角坐标系,通过平面![]() 和平面
和平面![]() 的法向量计算二面角的余弦值.
的法向量计算二面角的余弦值.
(1)因为![]() 平面
平面![]() ,所以
,所以![]() ,由于
,由于![]() ,
,![]() ,故
,故![]() 平面
平面![]() .(2)由于
.(2)由于![]() ,故
,故![]() 是靠近
是靠近![]() 的三等分点.以
的三等分点.以![]() 为坐标原点,建立如图所示的空间直角坐标系,依题意可知
为坐标原点,建立如图所示的空间直角坐标系,依题意可知![]() ,设
,设![]() ,则
,则![]() ,故
,故![]() ,解得
,解得![]() ,故
,故![]() ,且
,且![]() .由于
.由于![]() ,故
,故![]() 平面
平面![]() .故
.故![]() 是平面
是平面![]() 的法向量.设
的法向量.设![]() 是平面
是平面![]() 的法向量,则
的法向量,则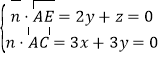 ,令
,令![]() ,解得
,解得![]() ,故
,故![]() .设二面角
.设二面角![]() 为
为![]() ,由图可知,
,由图可知,![]() 为钝角,故
为钝角,故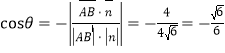 .所以二面角
.所以二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目