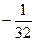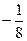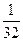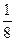题目内容
(本小题满分12分)
数列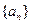 的前
的前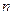 项和记为
项和记为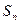 ,
,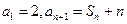 .
.
(Ⅰ)求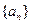 的通项公式;
的通项公式;
(Ⅱ)等差数列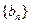 的各项为正,其前
的各项为正,其前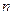 项和为
项和为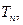 且
且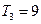 ,又
,又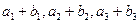 成
成
等比数列.
(1)求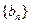 的通项公式;
的通项公式;
(2)求证:当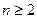 时,
时,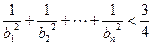 .
.
数列
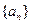 的前
的前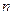 项和记为
项和记为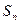 ,
,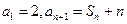 .
.(Ⅰ)求
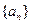 的通项公式;
的通项公式;(Ⅱ)等差数列
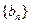 的各项为正,其前
的各项为正,其前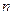 项和为
项和为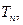 且
且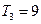 ,又
,又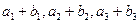 成
成等比数列.
(1)求
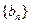 的通项公式;
的通项公式;(2)求证:当
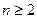 时,
时,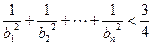 .
.(1)
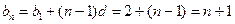
(2)略
解:(Ⅰ)由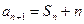 ,得
,得
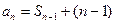
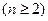 ,两式相减得
,两式相减得
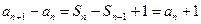 ,
,
所以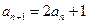 ------------------2分
------------------2分
所以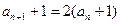
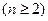 --------------3分
--------------3分
又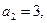 所以
所以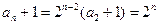 ,
,
从而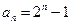
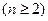 5分
5分
而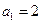 ,不符合上式,
,不符合上式,
所以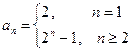 ------------6分
------------6分
(Ⅱ)(1)因为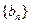 为等差数列,且前三项的和
为等差数列,且前三项的和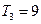 ,所以
,所以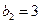 ,-------7分
,-------7分
可设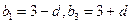
由于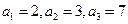 ,于是
,于是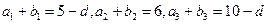 ,
,
因为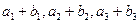 成等比数列,
成等比数列,
所以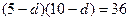 ,
,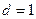 或
或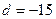 (舍)
(舍)
所以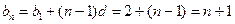 --------------9分
--------------9分
(2)因为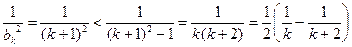
所以,当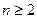 时
时
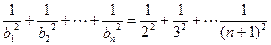
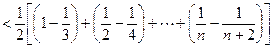
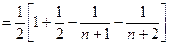
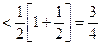 ----------------12分
----------------12分
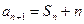 ,得
,得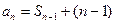
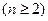 ,两式相减得
,两式相减得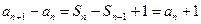 ,
,所以
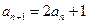 ------------------2分
------------------2分所以
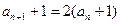
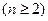 --------------3分
--------------3分又
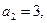 所以
所以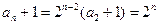 ,
,从而
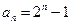
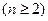 5分
5分而
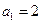 ,不符合上式,
,不符合上式,所以
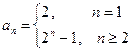 ------------6分
------------6分(Ⅱ)(1)因为
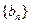 为等差数列,且前三项的和
为等差数列,且前三项的和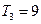 ,所以
,所以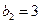 ,-------7分
,-------7分可设
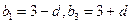
由于
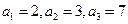 ,于是
,于是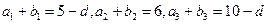 ,
,因为
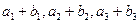 成等比数列,
成等比数列,所以
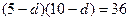 ,
,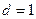 或
或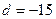 (舍)
(舍)所以
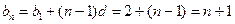 --------------9分
--------------9分(2)因为
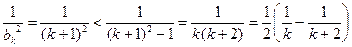
所以,当
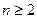 时
时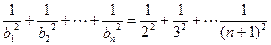
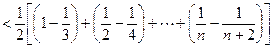
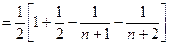
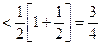 ----------------12分
----------------12分
练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
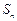 是数列
是数列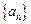 的前
的前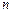 项和,
项和,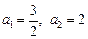 ,且
,且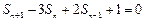 ,其中
,其中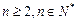 .
. 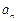 ; (2)计算
; (2)计算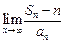 的值.
的值.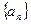 满足
满足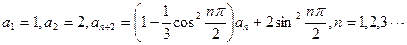
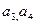 及数列
及数列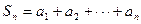 ,求
,求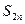 ;
;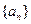 中,
中,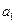 =1,
=1,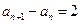 ,则
,则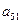 的值为( )
的值为( )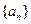 中,前
中,前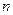 项和为
项和为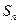 ,若
,若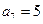 ,
,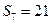 ,那么
,那么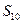 等于( )
等于( )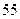
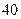
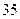
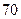
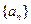 中,若
中,若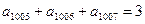 ,则该数列的前2011项的和为( )
,则该数列的前2011项的和为( )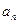 },有如下一个真命题:“若{
},有如下一个真命题:“若{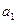 =0,s、
=0,s、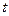 是互不相
是互不相 等的正整数,则
等的正整数,则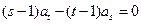 ”.类比此命题,对于等比数列{
”.类比此命题,对于等比数列{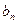 },有如下一个真命题:若{
},有如下一个真命题:若{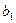 =1,s、
=1,s、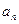 }中,
}中,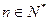 ,
,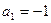 ,
,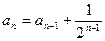 (
(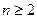 ),则
),则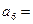 ( )
( )