题目内容
2.已知{an}是正项数列,a1=1,且点($\sqrt{{a}_{n}}$,an+1)(n∈N*)在函数y=x2+1的图象上.(1)求数列{an}的通项公式;
(2)若列数{bn}满足b1=1,bn+1=bn+2${\;}^{{a}_{n}}$,求证:bnbn+2<b${\;}_{n+1}^{2}$.
分析 (1)由题设条件知an+1=an+1,根据等差数列的定义即可求出数列的通项公式.
(2)根据数列的递推关系,利用累加法求出数列{bn}的表达式,即可比较大小.
解答 解:(1)∵点($\sqrt{{a}_{n}}$,an+1)(n∈N*)在函数y=x2+1的图象上
∴an+1=an+1,
即an+1-an=1,
则{an}是首项为1,公差为1的等差数列,
则an=n.
(2)若列数{bn}满足b1=1,bn+1=bn+2${\;}^{{a}_{n}}$,
则bn+1=bn+2${\;}^{{a}_{n}}$=bn+2n,
即bn+1-bn=2n,
则b2-b1=21,b3-b2=22,b4-b3=23,…bn-bn-1=2n-1,
等式两边同时相加得bn-b1=21+22+…+2n-1,
即bn=1+21+22+…+2n-1=$\frac{1•(1-{2}^{n})}{1-2}$=2n-1,
则bnbn+2=(2n-1)(2n+2-1)=22n+2-2n+2-2n+1=22n+2-5•2n+1
b${\;}_{n+1}^{2}$=(2n+1-1)2=2(2n+2)-2•2n+1+1=2(2n+2)-4•2n+1,
∴bnbn+2<b${\;}_{n+1}^{2}$.
点评 本题主要考查递推数列的应用,利用构造法和累加法,结合等差数列的定义,是解决本题的关键.

练习册系列答案
相关题目
14.y=cos2(2x)的最小正周期是( )
| A. | $\frac{π}{2}$ | B. | π | C. | 4π | D. | 8π |
17.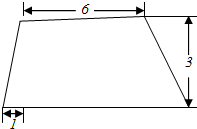 已知一圆台的轴截面如图所示,则它的内接四棱台体积的最大值为( )
已知一圆台的轴截面如图所示,则它的内接四棱台体积的最大值为( )
 已知一圆台的轴截面如图所示,则它的内接四棱台体积的最大值为( )
已知一圆台的轴截面如图所示,则它的内接四棱台体积的最大值为( )| A. | 37 | B. | 74 | C. | 111 | D. | 222 |
12.已知等差数列{an}满足a2=3,a5=9,若数列{bn}满足b1=3,bn+1=abn,则{bn}的通项公式为bn=( )
| A. | 2n-1 | B. | 2n+1 | C. | 2n+1-1 | D. | 2n-1+2 |
 如图,在正方形OABC内任取一点,取到函数y=x的图象与x轴正半轴之间(阴影部分)的点的概率等于0.5.
如图,在正方形OABC内任取一点,取到函数y=x的图象与x轴正半轴之间(阴影部分)的点的概率等于0.5.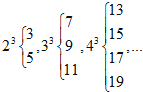 仿此,若m3的“分裂”数中有一个是73,则m的值为9.
仿此,若m3的“分裂”数中有一个是73,则m的值为9.