题目内容
已知函数 >0,ω>0,0<?<
>0,ω>0,0<?<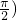 ,且y=f(x)的最大值为2,其图象相邻两对称轴间的距离为2,并过点(1,2).
,且y=f(x)的最大值为2,其图象相邻两对称轴间的距离为2,并过点(1,2).
(1)求?;
(2)计算f(1)+f(2)+…+f(2012).
解:(1)因为 ,y=f(x)的最大值为2,A>0,
,y=f(x)的最大值为2,A>0, ,∴A=2
,∴A=2
∵图象相邻两对称轴间的距离为2,ω>0, ,ω=
,ω= .
.
又函数过点(1,2).∴cos( ?)=-1,
?)=-1,
 ?=2kπ+π,k∈Z,∴?=k
?=2kπ+π,k∈Z,∴?=k ,k∈Z.∵0<?<
,k∈Z.∵0<?< ,所以?=
,所以?= .
.
(2)∵?= ,∴f(x)=1-cos(
,∴f(x)=1-cos( )=1+sin
)=1+sin .
.
∴f(1)+f(2)+f(3)+f(4)=2+1+0+1=4.
又易知y=f(x)的周期是4,2012=4×503,
∴f(1)+f(2)+…+f(2012)=4×503=2012.
分析:(1)通过函数的最大值,求出A,利用图象相邻两对称轴间的距离为2,求出函数的周期,通过函数图象过点(1,2).求?;
(2)利用(1)推出函数的解析式,通过函数的周期求出一个周期内的函数值,然后求f(1)+f(2)+…+f(2012).
点评:本题考查三角函数的解析式的求法,函数的周期的应用,函数值的求法,考查计算能力.
 ,y=f(x)的最大值为2,A>0,
,y=f(x)的最大值为2,A>0, ,∴A=2
,∴A=2∵图象相邻两对称轴间的距离为2,ω>0,
 ,ω=
,ω= .
.又函数过点(1,2).∴cos(
 ?)=-1,
?)=-1, ?=2kπ+π,k∈Z,∴?=k
?=2kπ+π,k∈Z,∴?=k ,k∈Z.∵0<?<
,k∈Z.∵0<?< ,所以?=
,所以?= .
.(2)∵?=
 ,∴f(x)=1-cos(
,∴f(x)=1-cos( )=1+sin
)=1+sin .
.∴f(1)+f(2)+f(3)+f(4)=2+1+0+1=4.
又易知y=f(x)的周期是4,2012=4×503,
∴f(1)+f(2)+…+f(2012)=4×503=2012.
分析:(1)通过函数的最大值,求出A,利用图象相邻两对称轴间的距离为2,求出函数的周期,通过函数图象过点(1,2).求?;
(2)利用(1)推出函数的解析式,通过函数的周期求出一个周期内的函数值,然后求f(1)+f(2)+…+f(2012).
点评:本题考查三角函数的解析式的求法,函数的周期的应用,函数值的求法,考查计算能力.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
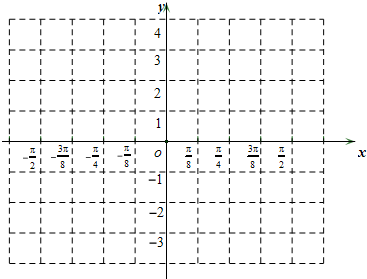 已知函数f(x)=sin2x+cos2x.
已知函数f(x)=sin2x+cos2x. 的定义域为
的定义域为 ,部分对应值如下表,
,部分对应值如下表, 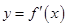 的图象如图所示.下列关于
的图象如图所示.下列关于

 ,
, ;
; 上是减函数;
上是减函数; 时,
时, 的最大值为4;
的最大值为4; 时,函数
时,函数 有
有