题目内容
已知椭圆椭圆C:
+
=1(a>b>0).定义圆心在原点O,半径为
的圆是椭圆C的“准圆”.若椭圆C的一个焦点为F(
,0),其短轴上的一个端点到F的距离为
.
(Ⅰ)求椭圆C的方程和其“准圆”方程;
(Ⅱ)点P是椭圆C的“准圆”上的一个动点,过动点P作直线l1,l2,使得l1,l2与椭圆C都只有一个交点,且l1,l2分别交其“准圆”于另一点M,N.求证:|MN|为定值.
| x2 |
| a2 |
| y2 |
| b2 |
| a2+b2 |
| 2 |
| 3 |
(Ⅰ)求椭圆C的方程和其“准圆”方程;
(Ⅱ)点P是椭圆C的“准圆”上的一个动点,过动点P作直线l1,l2,使得l1,l2与椭圆C都只有一个交点,且l1,l2分别交其“准圆”于另一点M,N.求证:|MN|为定值.
分析:(Ⅰ)直接由椭圆的简单几何性质得到a的值,结合c的值求出b的值,则椭圆C和其“准圆”的方程可求;
(Ⅱ)由椭圆的“准圆”与y轴的交点作为P点入手,分析得到|MN|的长为4,然后分过动点P的直线l1,l2的斜率一条不存在和两条直线的斜率都存在两种情况讨论,当其中一条直线的斜率不存在时,分析得到另一条的斜率等于0,说明过点P的两条直线互相垂直,当斜率都存在时,写出直线方程的点斜式,和椭圆方程联立后由根与系数关系得到两直线的斜率之积等于-1,也说明两直线垂直,所以得到结论M,N位于准圆的一条直径的两个端点上,即|MN|为定值4.
(Ⅱ)由椭圆的“准圆”与y轴的交点作为P点入手,分析得到|MN|的长为4,然后分过动点P的直线l1,l2的斜率一条不存在和两条直线的斜率都存在两种情况讨论,当其中一条直线的斜率不存在时,分析得到另一条的斜率等于0,说明过点P的两条直线互相垂直,当斜率都存在时,写出直线方程的点斜式,和椭圆方程联立后由根与系数关系得到两直线的斜率之积等于-1,也说明两直线垂直,所以得到结论M,N位于准圆的一条直径的两个端点上,即|MN|为定值4.
解答:解:(Ⅰ)∵c=
,短轴上的一个端点到F的距离为
.
∴a=
,∴b=1.∴椭圆方程为
+y2=1,
准圆的半径为
=2,
∴准圆方程为x2+y2=4.
(Ⅱ)(1)因为准圆x2+y2=4与y轴正半轴的交点为P(0,2),
设过点P(0,2)且与椭圆有一个公共点的直线为y=kx+2,
所以由
消去y,得(1+3k2)x2+12kx+9=0.
因为椭圆与y=kx+2只有一个公共点,
所以△=144k2-4×9(1+3k2)=0,解得k=±1.
所以l1,l2方程为y=x+2,y=-x+2.
则l1,l2与准圆的另一个交点分别为准圆与x轴的左右交点,|MN|=4.
(2)①当l1,l2中有一条无斜率时,不妨设l1无斜率,
因为l1与椭圆只有一个公共点,则其方程为x=±
,
当l1方程为x=
时,此时l1与准圆交于点(
,1),(
,-1),
此时经过点(
,1)(或(
,-1))且与椭圆只有一个公共点的直线是y=1(或y=-1),
即l2为y=1(或y=-1),显然直线l1,l2垂直;
同理可得l1方程为x=-
时,直线l1,l2垂直.
②当l1,l2都有斜率时,设点P(x0,y0),其中x02+y02=4.
设经过点P(x0,y0)与椭圆只有一个公共点的直线为y=t(x-x0)+y0,
则
,消去y得,(1+3t2)x2+6t(y0-tx0)x+3(y0-tx0)2-3=0.
由△=0化简整理得:(3-x02)t2+2x0y0t+1-y02=0.
因为x02+y02=4,所以有(3-x02)t2+2x0y0t+(x02-3)=0.
设l1,l2的斜率分别为t1,t2,因为l1,l2与椭圆只有一个公共点,
所以t1,t2满足上述方程(3-x02)t2+2x0y0t+(x02-3)=0,
所以t1•t2=-1,即l1,l2垂直.
综合①②知:因为l1,l2经过点P(x0,y0),又分别交其准圆于点M,N,且l1,l2垂直,
所以线段MN为准圆x2+y2=4的直径,所以|MN|=4.
综(1)、(2),|MN|为定值4.
| 2 |
| 3 |
∴a=
| 3 |
| x2 |
| 3 |
准圆的半径为
(
|
∴准圆方程为x2+y2=4.
(Ⅱ)(1)因为准圆x2+y2=4与y轴正半轴的交点为P(0,2),
设过点P(0,2)且与椭圆有一个公共点的直线为y=kx+2,
所以由
|
因为椭圆与y=kx+2只有一个公共点,
所以△=144k2-4×9(1+3k2)=0,解得k=±1.
所以l1,l2方程为y=x+2,y=-x+2.
则l1,l2与准圆的另一个交点分别为准圆与x轴的左右交点,|MN|=4.
(2)①当l1,l2中有一条无斜率时,不妨设l1无斜率,
因为l1与椭圆只有一个公共点,则其方程为x=±
| 3 |
当l1方程为x=
| 3 |
| 3 |
| 3 |
此时经过点(
| 3 |
| 3 |
即l2为y=1(或y=-1),显然直线l1,l2垂直;
同理可得l1方程为x=-
| 3 |
②当l1,l2都有斜率时,设点P(x0,y0),其中x02+y02=4.
设经过点P(x0,y0)与椭圆只有一个公共点的直线为y=t(x-x0)+y0,
则
|
由△=0化简整理得:(3-x02)t2+2x0y0t+1-y02=0.
因为x02+y02=4,所以有(3-x02)t2+2x0y0t+(x02-3)=0.
设l1,l2的斜率分别为t1,t2,因为l1,l2与椭圆只有一个公共点,
所以t1,t2满足上述方程(3-x02)t2+2x0y0t+(x02-3)=0,
所以t1•t2=-1,即l1,l2垂直.
综合①②知:因为l1,l2经过点P(x0,y0),又分别交其准圆于点M,N,且l1,l2垂直,
所以线段MN为准圆x2+y2=4的直径,所以|MN|=4.
综(1)、(2),|MN|为定值4.
点评:本题考查了椭圆的标准方程即简单几何性质,考查了直线与圆锥曲线的关系,是新定义题,考查了数形结合、分类讨论、函数与方程、等价转化等数学思想方法.第(Ⅱ)问学生不容易找到解题的方向.有些同学会忘记对斜率的讨论,对学生的方程思想要求比较高.属难题.

练习册系列答案
相关题目
 已知椭圆C:
已知椭圆C: (2012•枣庄二模)已知椭圆
(2012•枣庄二模)已知椭圆 (2012•枣庄二模)已知椭圆
(2012•枣庄二模)已知椭圆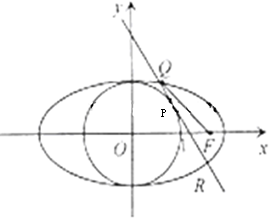 已知椭圆C:
已知椭圆C: