题目内容
设a,b,c,x,y,z均为正数,且a2+b2+c2=10,x2+y2+z2=40,ax+by+cz=20,则 等于( ).
等于( ).
A. | B. | C. | D. |
C
解析

练习册系列答案
相关题目
若 ,则函数
,则函数 的最大值为( )
的最大值为( )
A. | B. | C. | D. |
已知正整数a,b满足4a+b=30,则使得 +
+ 取最小值时的实数对(a,b)
取最小值时的实数对(a,b)
是 ( )
| A.(5,10) | B.(6,6) |
| C.(10,5) | D.(7,2) |
设x,y∈R+,且满足x+4y=40,则lgx+lgy的最大值为 ( )
| A.40 | B.10 | C.4 | D.2 |
设m>n,n∈N+,x>1,a=(lgx)m+(lgx)-m,b=(lgx)n+(lgx)-n,则a与b的大小关系为( )
| A.a≥b |
| B.a≤b |
| C.与x的值有关,大小不定 |
| D.以上都不正确 |
 的解集是 .
的解集是 . 对任意
对任意 恒成立,则实数
恒成立,则实数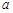 的取值范围是 .
的取值范围是 . -
- ,Q=
,Q= -
- ,a≥0,则P、Q的大小关系是________.
,a≥0,则P、Q的大小关系是________. 的大小关系为 .
的大小关系为 .