题目内容
已知椭圆 的焦点在
的焦点在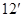 轴上,离心率为
轴上,离心率为 ,对称轴为坐标轴,且经过点
,对称轴为坐标轴,且经过点 .
.
(1)求椭圆 的方程;
的方程;
(2)直线 与椭圆
与椭圆 相交于
相交于 、
、 两点,
两点, 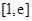 为原点,在
为原点,在 、
、 上分别存在异于
上分别存在异于 点的点
点的点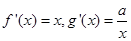 、
、 ,使得
,使得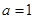 在以
在以 为直径的圆外,求直线斜率
为直径的圆外,求直线斜率 的取值范围.
的取值范围.
 的焦点在
的焦点在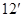 轴上,离心率为
轴上,离心率为 ,对称轴为坐标轴,且经过点
,对称轴为坐标轴,且经过点 .
.(1)求椭圆
 的方程;
的方程;(2)直线
 与椭圆
与椭圆 相交于
相交于 、
、 两点,
两点, 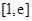 为原点,在
为原点,在 、
、 上分别存在异于
上分别存在异于 点的点
点的点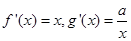 、
、 ,使得
,使得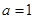 在以
在以 为直径的圆外,求直线斜率
为直径的圆外,求直线斜率 的取值范围.
的取值范围.(1)  (2)
(2) 
 (2)
(2) 
试题分析:(1)利用待定系数法设椭圆方程为
 ,然后利用题目条件建立方程,解方程即可;(2)联立直线与椭圆方程,得到关于x的一元二次方程,,然后利用韦达定理结合点在圆外
,然后利用题目条件建立方程,解方程即可;(2)联立直线与椭圆方程,得到关于x的一元二次方程,,然后利用韦达定理结合点在圆外 为锐角,即
为锐角,即 ,建立不等式求直线斜率
,建立不等式求直线斜率 的取值范围即可.
的取值范围即可.试题解析:(1)依题意,可设椭圆
 的方程为
的方程为 .
.由

∵ 椭圆经过点
 ,则
,则 ,解得
,解得
∴ 椭圆的方程为


(2)联立方程组
 ,消去
,消去 整理得
整理得

∵ 直线与椭圆有两个交点,
∴
 ,解得
,解得 ①
① 
∵ 原点
 在以
在以 为直径的圆外,∴
为直径的圆外,∴ 为锐角,即
为锐角,即 .
.而
 、
、 分别在
分别在 、
、 上且异于
上且异于 点,即
点,即

设
 两点坐标分别为
两点坐标分别为 ,
,则



解得
 , ②
, ② 
综合①②可知:


练习册系列答案
相关题目
 的右焦点重合,直线
的右焦点重合,直线 过点F交抛物线于A、B两点.
过点F交抛物线于A、B两点. ,m、n是实数,对于直线
,m、n是实数,对于直线 :
: 的离心率为
的离心率为 ,过椭圆
,过椭圆 的直线
的直线 与椭圆
与椭圆 (点
(点 为椭圆
为椭圆 的直线
的直线 与椭圆相交于
与椭圆相交于 两点.判断直线
两点.判断直线 是否关于直线
是否关于直线 对称,并说明理由.
对称,并说明理由. ,椭圆
,椭圆 以
以 的长轴为短轴,且与
的长轴为短轴,且与 为坐标原点,点
为坐标原点,点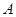 、
、 分别在椭圆
分别在椭圆 ,求直线
,求直线 的方程.
的方程. 的右焦点
的右焦点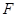 作相互垂直的两条弦
作相互垂直的两条弦 和
和 ,若
,若 的最小值为
的最小值为 ,则椭圆的离心率
,则椭圆的离心率 ( )
( )




 中,左焦点为
中,左焦点为 , 右顶点为
, 右顶点为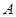 , 短轴上方端点为
, 短轴上方端点为 ,若
,若 ,则该椭圆的离心率为___________.
,则该椭圆的离心率为___________.
 +y2=1的左顶点为A,过A作两条互相垂直的弦AM、AN交椭圆于M、N两点.
+y2=1的左顶点为A,过A作两条互相垂直的弦AM、AN交椭圆于M、N两点. 的直线l与椭圆
的直线l与椭圆 =1(a>b>0)有两个不同的交点,且这两个交点在x轴上的射影恰好是椭圆的两个焦点,则该椭圆的离心率为________.
=1(a>b>0)有两个不同的交点,且这两个交点在x轴上的射影恰好是椭圆的两个焦点,则该椭圆的离心率为________. =1的焦距为2,求椭圆上的一点到两个焦点的距离之和.
=1的焦距为2,求椭圆上的一点到两个焦点的距离之和.