题目内容
10.已知函数y=f(x)的图象与函数y=logax(a>0且a≠1)的图象关于直线y=x对称,如果函数g(x)=f(x)[f(x)-3a2-1](a>0,且a≠1)在区间[0,+∞)上是增函数,那么a的取值范围是( )| A. | [0,$\frac{2}{3}$] | B. | [$\frac{\sqrt{3}}{3}$,1) | C. | [1,$\sqrt{3}$] | D. | [$\frac{3}{2}$,+∞) |
分析 由已知函数g(x)=ax(ax-3a2-1)(a>0且a≠1)在区间[0,+∞)上是增函数,令ax=t,利用换元法及二次函数性质能求出a的取值范围.
解答 解:∵函数y=f(x)的图象与函数y=logax(a>0且a≠1)的图象关于直线y=x对称,
∴f(x)=ax(a>0,a≠1),
∵函数g(x)=f(x)[f(x)-3a2-1](a>0,且a≠1)在区间[0,+∞)上是增函数,
∴函数g(x)=ax(ax-3a2-1)(a>0且a≠1)在区间[0,+∞)上是增函数
令ax=t,则g(x)=ax(ax-3a2-1)转化为y=t2-(3a2+1)t,其对称轴为t=$\frac{3{a}^{2}+1}{2}$>0,
当a>1时,t≥1,要使函数y=t2-(3a2+1)t在[1,+∞)上是增函数
则t=$\frac{3{a}^{2}+1}{2}$≤1,故不存在a使之成立;
当0<a<1时,0<t≤1,要使函数y=t2-(3a2+1)t在(0,1]上是减函数
则t=$\frac{3{a}^{2}+1}{2}$≥1,故$\frac{\sqrt{3}}{3}$≤a<1.
综上所述,a的取值范围是[$\frac{\sqrt{3}}{3}$,1).
故选:B.
点评 本题考查实数的取值范围的求法,是基础题,解题时要认真审题,注意换元法及二次函数性质的合理运用.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
1.已知$sin(α+\frac{π}{3})=\frac{1}{3}$,则$cos(\frac{π}{6}-α)$=( )
| A. | $-\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $-\frac{{2\sqrt{3}}}{3}$ |
5.执行如图的框图,第3次和最后一次输出的A的值是( )
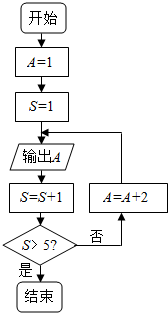

| A. | 7,9 | B. | 5,11 | C. | 7,11 | D. | 5,9 |
2.若定义在R上的函数f(x)满足f(0)=-1,g(x)=f(x)-kx,h(x)=f(x)-x,且函数g(x)与函数h(x)在R上均单调递增,当k>l时,则下列结论中一定错误的是( )
| A. | $f({\frac{1}{k}})<\frac{1}{k}$ | B. | $f({\frac{1}{k}})>\frac{1}{k-1}$ | C. | $f({\frac{1}{k-1}})>\frac{1}{k-1}$ | D. | $f({\frac{1}{k-1}})<\frac{1}{k-1}$ |