题目内容
20.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,短轴一个端点到右焦点F的距离为2.(Ⅰ)求椭圆C的方程;
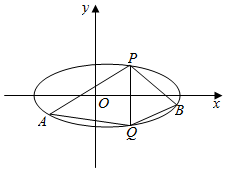
(Ⅱ)设点P($\sqrt{3}$,$\frac{1}{2}$),过点F的直线l与椭圆C交于A,B两点,与直线x=m(m>a)交于M点,若直线PA,PM,PB的斜率成等差数列,求m的值.
分析 (Ⅰ)运用离心率公式和a,b,c的关系,解得a=2,b=1,即可得到所求椭圆方程;
(Ⅱ)由F($\sqrt{3}$,0),设直线AB的方程为y=k(x-$\sqrt{3}$),代入椭圆方程,运用韦达定理,以及等差数列的中项性质,和直线的斜率公式,计算化简即可得到所求值.
解答 解:(Ⅰ)由题意可得e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,a=$\sqrt{{b}^{2}+{c}^{2}}$=2,
可得c=$\sqrt{3}$,b=1,
即有椭圆的方程为$\frac{{x}^{2}}{4}$+y2=1;
(Ⅱ)由F($\sqrt{3}$,0),设直线AB的方程为y=k(x-$\sqrt{3}$),
代入椭圆方程x2+4y2=4,可得
(1+4k2)x2-8$\sqrt{3}$k2x+12k2-4=0,
设A(x1,y1),B(x2,y2),
可得x1+x2=$\frac{8\sqrt{3}{k}^{2}}{1+4{k}^{2}}$,x1x2=$\frac{12{k}^{2}-4}{1+4{k}^{2}}$,
设M(m,k(m-$\sqrt{3}$)),
由直线PA,PM,PB的斜率成等差数列,可得
2•$\frac{k(m-\sqrt{3})-\frac{1}{2}}{m-\sqrt{3}}$=$\frac{{y}_{1}-\frac{1}{2}}{{x}_{1}-\sqrt{3}}$+$\frac{{y}_{2}-\frac{1}{2}}{{x}_{2}-\sqrt{3}}$=$\frac{k({x}_{1}-\sqrt{3})-\frac{1}{2}}{{x}_{1}-\sqrt{3}}$+$\frac{k({x}_{2}-\sqrt{3})-\frac{1}{2}}{{x}_{2}-\sqrt{3}}$
即为2k-$\frac{1}{m-\sqrt{3}}$=2k-$\frac{1}{2}$•$\frac{{x}_{1}+{x}_{2}-2\sqrt{3}}{{x}_{1}{x}_{2}+3-\sqrt{3}({x}_{1}+{x}_{2})}$,
代入韦达定理,可得$\frac{1}{m-\sqrt{3}}$=$\sqrt{3}$,
解得m=$\frac{4\sqrt{3}}{3}$.
点评 本题考查椭圆的方程的求法,注意运用离心率公式和a,b,c的关系,考查直线和椭圆方程联立,运用韦达定理,以及等差数列的中项性质,和直线的斜率公式,考查运算能力,属于中档题.

| A. | [0,$\frac{2}{3}$] | B. | [$\frac{\sqrt{3}}{3}$,1) | C. | [1,$\sqrt{3}$] | D. | [$\frac{3}{2}$,+∞) |
| 广告支出x/万元 | 1 | 2 | 3 | 4 |
| 销售收入y/万元 | 12 | 28 | 42 | 56 |
| $\overline{x}$ | $\overline{y}$ | $\sum_{i=1}^{4}$($\overline{x}$i-$\overline{x}$)2 | $\sum_{i=1}^{4}$($\overline{x}$i-$\overline{x}$)(yi-$\overline{y}$) |
| $\frac{5}{2}$ | $\frac{69}{2}$ | 5 | 73 |
(1)画出表中数据的散点图;
(2)求出y与x的回归直线方程;
(3)若广告费为9万元,则销售收入约为多少?
 如图是我校100名高三学生第6次月考考试数学成绩的频率分布直方图,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
如图是我校100名高三学生第6次月考考试数学成绩的频率分布直方图,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].(1)求图中a的值和这100名学生数学成绩的平均数;
(2)若这100名学生数学成绩某些分数段的人数(x)与地理成绩相应分数段的人数(y)之比如表所示,求地理成绩在[50,90)之外的人数.
| 分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
| x:y | 1:1 | 2:1 | 3:4 | 4:5 |
| A. | (-∞,3) | B. | (-∞,1) | C. | (-1,+∞) | D. | (-3,+∞) |
 已知椭圆C的中心在原点,焦点在x轴上,离心率等于$\frac{{\sqrt{3}}}{2}$,它的两个顶点恰好是双曲线y2-x2=1的两个焦点.
已知椭圆C的中心在原点,焦点在x轴上,离心率等于$\frac{{\sqrt{3}}}{2}$,它的两个顶点恰好是双曲线y2-x2=1的两个焦点. 如图,某景区有一座高AD为1千米的山,山顶A处可供游客观赏日出.坡角∠ACD=30°,在山脚有一条长为10千米的小路BC,且BC与CD垂直,为方便游客,该景区拟在小路BC上找一点M,建造两条直线型公路BM和MA,其中公路BM每千米的造价为30万元,公路MA每千米的造价为60万元.
如图,某景区有一座高AD为1千米的山,山顶A处可供游客观赏日出.坡角∠ACD=30°,在山脚有一条长为10千米的小路BC,且BC与CD垂直,为方便游客,该景区拟在小路BC上找一点M,建造两条直线型公路BM和MA,其中公路BM每千米的造价为30万元,公路MA每千米的造价为60万元.