题目内容
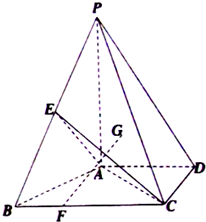 (2012•道里区二模)已知四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是直角梯形,∠ADC=90°,AD∥BC,AB⊥AC,AB=AC=2,G为△PAC的重心,E为PB的中点,F在BC上,且CF=2FB.
(2012•道里区二模)已知四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是直角梯形,∠ADC=90°,AD∥BC,AB⊥AC,AB=AC=2,G为△PAC的重心,E为PB的中点,F在BC上,且CF=2FB.(1)求证:FG∥平面PAB;
(2)当FG⊥平面AEC时,求二面角P-CD-A的正切值.
分析:(1)欲证FG∥平面PAB,根据直线与平面平行的判定定理可知只需证FG与平面PAB内一直线平行,连接CG延长交PA于M,连BM,根据比例可得FG∥BM,BM?平面PAB,FG?平面PAB,满足定理条件;
(2)连EM,根据二面角平面角的定义可知∠PDA二面角P-CD-A的平面角,在△PDA中求出此角的正切值即可.
(2)连EM,根据二面角平面角的定义可知∠PDA二面角P-CD-A的平面角,在△PDA中求出此角的正切值即可.
解答:(1)证明:连接CG交AP于M点
∵G为△PAC的重心,∴
=
=
,∴FG∥BM,
又BM?平面PAB,∴FG∥平面PAB…(4分)
(2)解:因为PA⊥平面ABCD,所以AD⊥CD,所以PD⊥CD,所以∠PDA即为二面角的平面角 …(6分)
在直角梯形ABCD中,ADC=90°,AD∥BC,AB⊥AC,AB=AC=2,所以AD=
…(7分)
连BM,连EM,
∵FG⊥平面AEC,∴FG⊥AE,即BM⊥AE,又EM=
AB=1,
设EA∩BM=H,则EH=
HA,
设PA=h,则EA=
PB=
,EH=
EA=
,
∵Rt△AME~Rt△MHE,
∴EM2=EH•EA.
∴
•
=1,
∴h=2
,即PA=2
…(9分)
∴tan∠PAD=
=2…(12分)
∵G为△PAC的重心,∴
| CG |
| GM |
| CF |
| BF |
| 2 |
| 1 |
又BM?平面PAB,∴FG∥平面PAB…(4分)
(2)解:因为PA⊥平面ABCD,所以AD⊥CD,所以PD⊥CD,所以∠PDA即为二面角的平面角 …(6分)
在直角梯形ABCD中,ADC=90°,AD∥BC,AB⊥AC,AB=AC=2,所以AD=
| 2 |
连BM,连EM,
∵FG⊥平面AEC,∴FG⊥AE,即BM⊥AE,又EM=
| 1 |
| 2 |

设EA∩BM=H,则EH=
| 1 |
| 2 |
设PA=h,则EA=
| 1 |
| 2 |
| 1 |
| 2 |
| 4+h2 |
| 1 |
| 3 |
| 1 |
| 6 |
| 4+h2 |
∵Rt△AME~Rt△MHE,
∴EM2=EH•EA.
∴
| 1 |
| 2 |
| 4+h2 |
| 1 |
| 2 |
| 4+h2 |
∴h=2
| 2 |
| 2 |
∴tan∠PAD=
| PA |
| AD |
点评:本题主要考查了空间中直线与直线之间的位置关系,以及直线与平面平行的判定,考查面面角,属于中档题.

练习册系列答案
相关题目
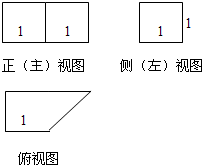 (2012•道里区二模)一个几何体的三视图如图所示,则该几何体的体积为( )
(2012•道里区二模)一个几何体的三视图如图所示,则该几何体的体积为( )