题目内容
已知椭圆![]() 的中心在原点,长轴在
的中心在原点,长轴在![]() 轴上,若椭圆上有一点
轴上,若椭圆上有一点![]() 到两焦点的距离分别是
到两焦点的距离分别是![]() 和
和![]() ,且过点
,且过点![]() 作长轴的垂线恰好过椭圆的一个焦点.
作长轴的垂线恰好过椭圆的一个焦点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)试探究椭圆![]() 上是否存在两点
上是否存在两点![]() 关于直线
关于直线![]() 对称,如果存在,求出实数
对称,如果存在,求出实数![]() 的取值范围;如果不存在,请说明理由.
的取值范围;如果不存在,请说明理由.
解:(Ⅰ)设所求椭圆的方程为![]() ,两焦点
,两焦点![]() 的距离
的距离![]()
∵![]() ,∴
,∴![]()
又![]() 为直角三角形,
为直角三角形,![]() 为直角边
为直角边
∴![]() ,∴
,∴![]() ,
,![]()
∴所求椭圆方程为![]()
(Ⅱ) 方法一:假设椭圆![]() 上存在两点
上存在两点![]() 关于直线
关于直线![]() 对称,设直线
对称,设直线![]() 的方程为
的方程为![]() .
.
联立方程组得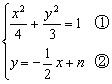
消取![]() 得
得![]()
整理得![]() ③
③
设![]() 两点的坐标分别是
两点的坐标分别是![]() 和
和![]() ,则
,则
![]() 是方程③的两个不相等的实根
是方程③的两个不相等的实根
∴![]() ,
,
∴![]() ④
④
又设![]() 是
是![]() 的中点,
的中点,
∴![]() ,∴
,∴![]()
又点![]() 在对称轴
在对称轴![]() 上
上
∴![]() ,
,
∴![]() ⑤
⑤
把⑤代入④得![]() ,∴
,∴![]()
故椭圆![]() 上存在两点
上存在两点![]() 关于直线
关于直线![]() 对称,实数
对称,实数![]() 的取值范围是
的取值范围是![]() .
.
方法二:假设椭圆![]() 上存在两点
上存在两点![]() 关于直线
关于直线![]() 对称,设
对称,设![]() 的中点为
的中点为![]() ,则
,则
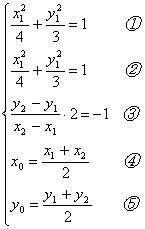
由①-②得![]() ⑥
⑥
把③④⑤代入⑥得![]()
又![]() ,
,
∴![]()
又点![]() 在椭圆内
在椭圆内
∴![]()
∴![]()
∴![]()
∴![]()
故椭圆![]() 上存在两点
上存在两点![]() 关于直线
关于直线![]() 对称,实数
对称,实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目