Question

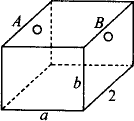
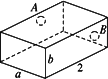
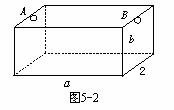
如图5-2，为处理含有某种杂质的污水，要制造一底宽为2米的无盖长方体沉淀箱，污水从A孔流入，经沉淀后从B孔流出，设箱体的长度为a米，高度为b米.已知流出的水中该杂质的质量分数与a、b的乘积ab成反比.现有制箱材料60平方米.问当a、b各为多少米时，经沉淀后流出的水中该杂质的质量分数最小(A、B孔的面积忽略不计)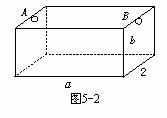

Answer 1

解法一：设y为流出的水中杂质的质量分数，则y=，

其中k＞0为比例系数，依题意，即所求的a、b值使y值最小.?

根据题设，有4b+2ab+2a=60 (a＞0，b＞0）

 

得b=（0＜a＜30）①

 

于是y=≥

 

当a+2=时取等号，y达到最小值.

这时a=6, a=-10(舍去)将a=6代入①式得b=3

故当a为6米，b为3米时，经沉淀后流出的水中该杂质的质量分数最小.?

 

解法二：

依题意，即所求的a、b值使ab最大.?

由题设知4b+2ab+2a=60 (a＞0，b＞0）?

即a+2b+ab=30 (a＞0，b＞0）?

∵a+2b≥2∴2＋ab≤30

当且仅当a=2b时，上式取等号.

由a＞0，b＞0，解得0＜ab≤18

即当a=2b时，ab取得最大值，其最大值为18.?

∴2b²＝18．解得b=3,a=6.?

故当a为6米，b为3米时，经沉淀后流出的水中该杂质的质量分数最小.?

评述：本题考查综合应用所学数学知识、思想和方法解决实际问题的能力，考查函数关系、不等式性质、最大值、最小值等基础知识.考查利用均值不等式求最值的方法、阅读理解能力、建模能力.