题目内容
定义在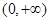 上的可导函数
上的可导函数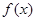 满足:
满足: 且
且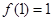 ,则不等式
,则不等式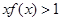 的解集为( )
的解集为( )
A.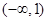 | B.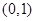 | C.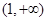 | D. |
B
解析试题分析:设 ,则
,则 ,所以
,所以 在
在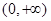 上单调递减,又因为
上单调递减,又因为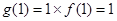 ,所以不等式
,所以不等式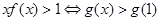 ,根据
,根据 在
在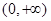 上单调递减,可知
上单调递减,可知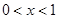 ,故选B.
,故选B.
考点:1.函数的单调性与导数;2.函数的单调性在求解不等式中的应用.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
现有四个函数:①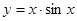 ;②
;②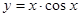 ;③
;③ ; ④
; ④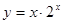 的图象(部分)如下,但顺序被打乱,则按照从左到右的顺序对应的函数序号是( )
的图象(部分)如下,但顺序被打乱,则按照从左到右的顺序对应的函数序号是( )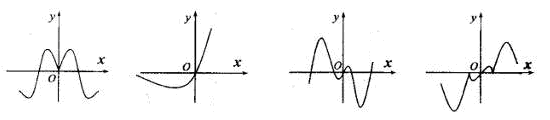
| A.④①②③ | B.①④②③ | C.①④③② | D.③④②① |
设定义域为R的函数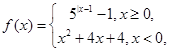 若关于x的方程
若关于x的方程 有7个不同的实数解,则m=( ).
有7个不同的实数解,则m=( ).
| A.2 | B.4或6 | C.2或6 | D.6 |
已知函数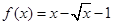 ,
,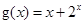 ,
, 的零点分别为
的零点分别为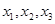 ,则( )
,则( )
A.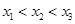 | B.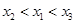 | C.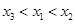 | D.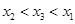 |
若f(x)为奇函数,且在(-∞,0)内是增函数,又f(-2)=0,则xf(x)<0的解集为( )
| A.(-2,0)∪(0,2) | B.(-∞,-2)∪(0,2) |
| C.(-∞,-2)∪(2,+∞) | D.(-2,0)∪(2,+∞) |
定义在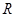 上的函数
上的函数 满足
满足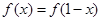 ,且当
,且当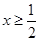 时,
时,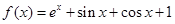 ,则有( )
,则有( )
A.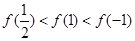 |
B.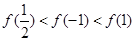 |
C.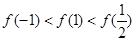 |
D.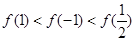 |
若函数f(x)=x2-2x,g(x)=ax+2(a>0),?x1∈[-1,2],?x0∈[-1,2],使g(x1)=f(x0),则a的取值范围是( )
A.(0,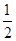 ] ] | B.[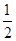 ,3] ,3] | C.[3,+∞) | D.(0,3] |
 的大致图像是( )
的大致图像是( )