题目内容
(本小题满分12分)如图,在直三棱柱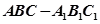 中,
中,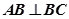 ,
,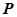 为
为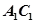 的中点,且
的中点,且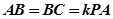 ,
,
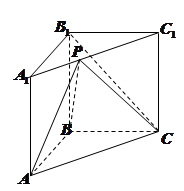
(1)当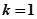 时,求证:
时,求证: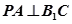 ;
;
(2)当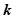 为何值时,直线
为何值时,直线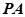 与平面
与平面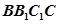 所成的角的正弦值为
所成的角的正弦值为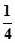 ,并求此时二面角
,并求此时二面角
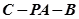 的余弦值。
的余弦值。
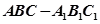 中,
中,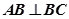 ,
,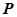 为
为 的中点,且
的中点,且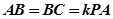 ,
,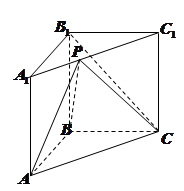
(1)当
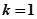 时,求证:
时,求证: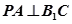 ;
;(2)当
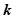 为何值时,直线
为何值时,直线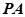 与平面
与平面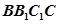 所成的角的正弦值为
所成的角的正弦值为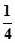 ,并求此时二面角
,并求此时二面角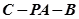 的余弦值。
的余弦值。(1)见解析;(2)二面角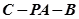 的余弦值为
的余弦值为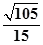
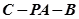 的余弦值为
的余弦值为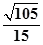
第一问中设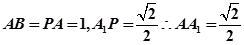 ,建系
,建系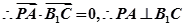
第二问,设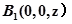 则
则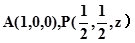 ,
,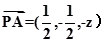
易知面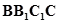 的法向量
的法向量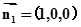 设直线
设直线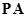 与平面
与平面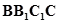 所成角为
所成角为 ,
,
则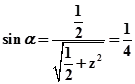 ,
,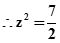 ,
,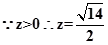 ,
,  ,
,
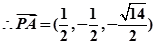 ,
,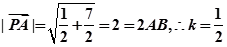
设面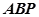 的法向量
的法向量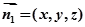
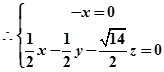
则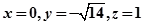 ,
, 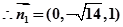
利用两平面的法向量得到二面角的平面角。
解:(1)设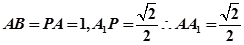 ,如图建系,则
,如图建系,则
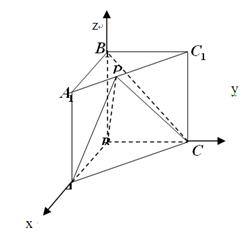
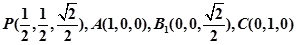 ,
,
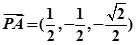 ,
,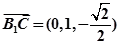
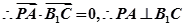 …...4
…...4
(2)设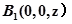 则
则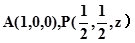 ,
,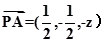
易知面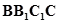 的法向量
的法向量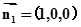 设直线
设直线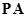 与平面
与平面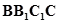 所成角为
所成角为 ,
,
则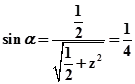 ,
,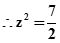 ,
,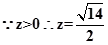 ,
,  ,
,
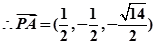 ,
,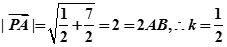 ...8
...8
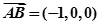 设面
设面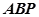 的法向量
的法向量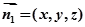
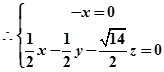
则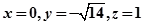 ,
, 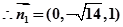 ......9
......9
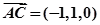 设面
设面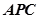 的法向量
的法向量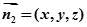
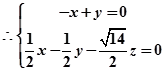 则
则
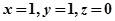 ,
,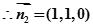 设二面角
设二面角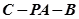 的大小为
的大小为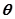 则
则
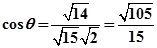
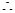 二面角
二面角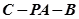 的余弦值为
的余弦值为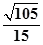 ...12
...12
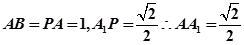 ,建系
,建系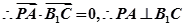
第二问,设
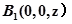 则
则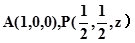 ,
,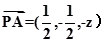
易知面
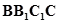 的法向量
的法向量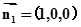 设直线
设直线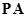 与平面
与平面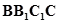 所成角为
所成角为 ,
,则
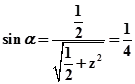 ,
,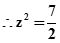 ,
,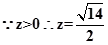 ,
,  ,
,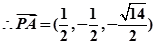 ,
,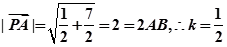
设面
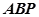 的法向量
的法向量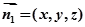
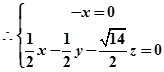
则
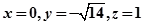 ,
, 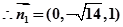
利用两平面的法向量得到二面角的平面角。
解:(1)设
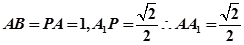 ,如图建系,则
,如图建系,则
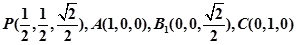 ,
,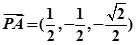 ,
,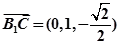
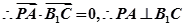 …...4
…...4 (2)设
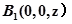 则
则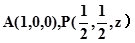 ,
,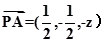
易知面
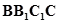 的法向量
的法向量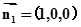 设直线
设直线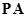 与平面
与平面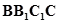 所成角为
所成角为 ,
,则
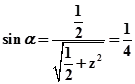 ,
,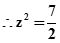 ,
,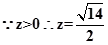 ,
,  ,
,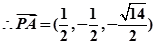 ,
,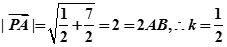 ...8
...8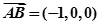 设面
设面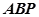 的法向量
的法向量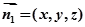
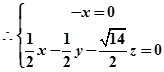
则
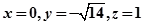 ,
, 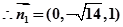 ......9
......9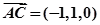 设面
设面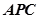 的法向量
的法向量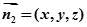
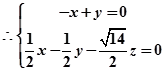 则
则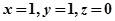 ,
,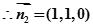 设二面角
设二面角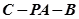 的大小为
的大小为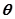 则
则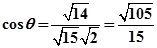
 二面角
二面角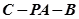 的余弦值为
的余弦值为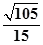 ...12
...12
练习册系列答案
相关题目
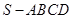 中,底面
中,底面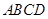 是正方形,其他四个侧面都是等边三角形,
是正方形,其他四个侧面都是等边三角形,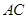 与
与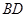 的交点为
的交点为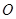 ,
,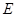 为侧棱
为侧棱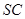 上一点.
上一点.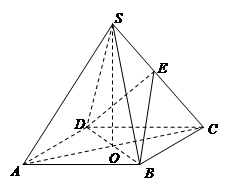
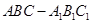 中,
中,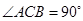 ,
,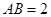 ,
,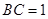 ,
,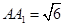 ,点
,点 是棱
是棱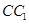 的中点.
的中点.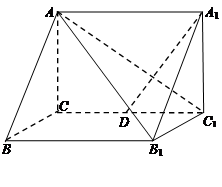
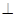 平面
平面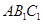 ;
;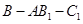 的余弦值.
的余弦值. 为正方形,
为正方形,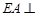 平面
平面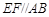 ,
,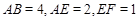 .
.
 在线段
在线段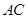 上,且满足
上,且满足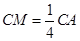 ,求证:
,求证: 平面
平面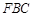 ;
;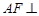 平面
平面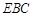 ;
; 的余弦值.
的余弦值.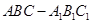 中,
中,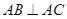 ,
,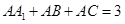 ,
,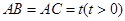 ,
,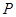 是侧棱
是侧棱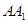 上的动点.
上的动点.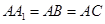 时,求证:
时,求证: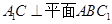 ;
; 的平面角的余弦值为
的平面角的余弦值为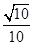 ,试求实数
,试求实数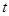 的值.
的值.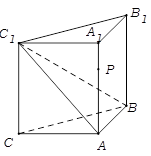
 ,侧面PAB是等边三角形,且侧面PAB⊥底面ABCD.
,侧面PAB是等边三角形,且侧面PAB⊥底面ABCD. 

 中,底面
中,底面 为矩形,平面
为矩形,平面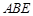 ,
,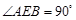 ,
,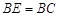 ,
,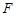 为
为 的中点,
的中点,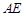 ∥平面
∥平面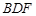 ;(2)平面
;(2)平面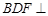 平面
平面 .
.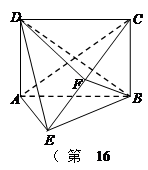
 ,直线
,直线 ,则下列四个命题:①
,则下列四个命题:①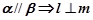 ;②
;② ;③
;③ ;④
;④ .其中正确的是( ).
.其中正确的是( ).