题目内容
已知过点A(-4,0)的动直线l与抛物线G:x2=2py(p>0)相交于B,C两点.当直线l的斜率是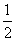 时,
时,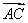 =4
=4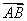 .
.
(1)求抛物线G的方程;
(2)设线段BC的中垂线在y轴上的截距为b,求b的取值范围.
解:(1)设B(x1,y1),C(x2,y2),当直线l的斜率为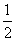 时,l的方程为y=
时,l的方程为y=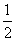 (x+4),即x=2y-4.
(x+4),即x=2y-4.
由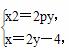 得2y2-(8+p)y+8=0,
得2y2-(8+p)y+8=0,
∴
又∵ =4
=4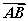 ,∴y2=4y1,③
,∴y2=4y1,③
由①②③及p>0得:y1=1,y2=4,p=2,
则抛物线G的方程为x2=4y.
(2)设l:y=k(x+4),
BC的中点坐标为(x0,y0),
由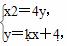 得x2-4kx-16k=0,④
得x2-4kx-16k=0,④
∴x0=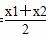 =2k,
=2k,
y0=k(x0+4)=2k2+4k.
∴线段BC的中垂线方程为
y-2k2-4k=-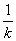 (x-2k),
(x-2k),
∴线段BC的中垂线在y轴上的截距为:
b=2k2+4k+2=2(k+1)2,
对于方程④,由Δ=16k2+64k>0得k>0或k<-4.∴b∈(2,+∞).
故b的取值范围为(2,+∞).

 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案对照研究又称为回顾性研究,是在已经发病之后来研究发病的原因.具体做法:将患有某种疾病(或具有某种特征)的人分为一组,称为病例组;将非病(或不具有某种特征)的人分为另一组,称为对照组.对每一组研究对象都可以获得过去接触危险因素的比例或水平,从而分析和推导发病与危险因素之间的联系.为研究血液中儿茶酚胺含量的高低与冠心病的发病之间的关系,有人进行了对照研究.对609名男子测定血液中儿茶酚胺水平(分为高、低两类),随之经过10年追踪观察取得了冠心病的发病资料,见下表:
|
| 发病 | 未发病 | 合计 |
| 儿茶酚胺水平高 | 27 | 95 | 122 |
| 儿茶酚胺水平低 | 44 | 443 | 487 |
| 合计 | 71 | 538 | 609 |
试分析血液中儿茶酚胺含量的高低与冠心病的发病之间是否有关?
某公司生产产品A,产品质量按测试指标分为:指标大于或等于90为一等品,大于或等于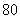 小于
小于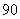 为二等品,小于
为二等品,小于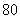 为三等品,生产一件一等品可盈利50元,生产一件二等品可盈利
为三等品,生产一件一等品可盈利50元,生产一件二等品可盈利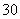 元,生产一件三等品亏损10元.现随机抽查熟练工人甲和新工人乙生产的这种产品各100件进行检测,检测结果统计如下:
元,生产一件三等品亏损10元.现随机抽查熟练工人甲和新工人乙生产的这种产品各100件进行检测,检测结果统计如下:
| 测试指标 |
|
|
|
|
|
|
| 甲 | 3 | 7 | 20 | 40 | 20 | 10 |
| 乙 | 5 | 15 | 35 | 35 | 7 | 3 |
现将根据上表统计得到甲、乙两人生产产品A为一等品、二等品、三等品的频率分别估计为他们生产产品A为一等品、二等品、三等品的概率.
(1)计算新工人乙生产三件产品A,给工厂带来盈利大于或等于100元的概率;
(2)记甲乙分别生产一件产品A给工厂带来的盈利和记为X,求随机变量X的概率分布和数学期望.
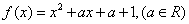 .
. 时,解不等式:
时,解不等式: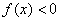 ;
;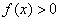 对x∈R恒成立,求实数
对x∈R恒成立,求实数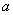 的取值范围.
的取值范围. (-3,3),
(-3,3), (-5,-1),那么
(-5,-1),那么 等于( )
等于( )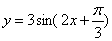 的图像可以看作是把函数
的图像可以看作是把函数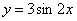 的图像作下列移动而得到( )
的图像作下列移动而得到( )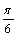 个单位长度 B.向右平移
个单位长度 B.向右平移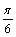 个单位长度
个单位长度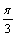 个单位长度 D.向右平移
个单位长度 D.向右平移 .
. 的单调区间;
的单调区间; 在点
在点 处的切线方程;
处的切线方程; 所围成的图形的面积
所围成的图形的面积 .
.




