Question

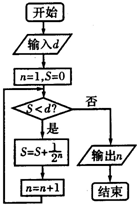等差数列{a_n}满足：a₃=1，a₈=5，公差为d，则按右侧程序框图运行时，得到的n=

5

．

Answer 1

分析：先根据条件求出公差，再根据循环结构一次次计算，一直到满足要求即可求出答案．

解答：解：因为等差数列{a_n}满足：a₃=1，a₈=5，
∴5d=a₈-a₃=4；
∴d=

4

5

．
开始n=1，s=0；
第一次：s=0+

1

21

=

1

2

，n=2；
第二次：s=

1

2

+

1

22

=

5

8

，n=3；
第三次：s=

5

8

+

1

23

=

6

8

=

3

4

，n=4；
第四次：s=

3

4

+

1

24

=

13

16

＞

4

5

，n=5，
故答案为：5．

点评：本题考查循环结构，解题的关键是理解框图，由框图得出算法，再由所得的算法进行计算得出答案，本题有形入数，是对框图进行考查的主要题型．在近几年的高考中多以选择填空题的形式出现．