题目内容
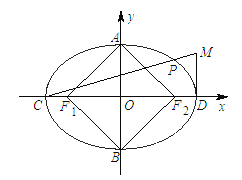
【题目】已知椭圆![]() 的左.右焦点分别为
的左.右焦点分别为![]() ,短轴两个端点为
,短轴两个端点为![]() ,且四边形
,且四边形![]() 的边长为
的边长为![]() 的正方形.
的正方形.
(Ⅰ)求椭圆的方程;
(Ⅱ)若![]() ,分别是椭圆长轴的左,右端点,动点
,分别是椭圆长轴的左,右端点,动点![]() 满足
满足![]() ,连结
,连结![]() ,交椭圆于点
,交椭圆于点![]() .证明:
.证明: ![]() 的定值;
的定值;
(Ⅲ)在(Ⅱ)的条件下,试问![]() 轴上是否存在异于点
轴上是否存在异于点![]() ,的定点
,的定点![]() ,使得以
,使得以![]() 为直径的圆恒过直线
为直径的圆恒过直线![]() ,
,![]() 的交点,若存在,求出点
的交点,若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【答案】(Ⅰ) ![]() ;(Ⅱ)见解析;(Ⅲ) 存在
;(Ⅱ)见解析;(Ⅲ) 存在![]() ,使得以
,使得以![]() 为直径的圆恒过直线
为直径的圆恒过直线![]() ,
,![]() 的交点.
的交点.
【解析】
试题(I)由于四边形为正方形,所以![]() ,由此求得椭圆方程为
,由此求得椭圆方程为![]() .(II)设出直线
.(II)设出直线![]() 的方程,联立直线方程和椭圆方程,求出
的方程,联立直线方程和椭圆方程,求出![]() 点坐标,代入
点坐标,代入![]() 可求得值为
可求得值为![]() .(III)设出
.(III)设出![]() 点的坐标,利用圆的直径所对圆周角为直角的几何性质得到
点的坐标,利用圆的直径所对圆周角为直角的几何性质得到![]() ,结合(II)将
,结合(II)将![]() 的坐标代入上式,可求得
的坐标代入上式,可求得![]() .
.
试题解析:(Ⅰ)由题意得, ![]()
![]() ,
,![]()
所以所求的椭圆方程为![]()
(Ⅱ)由(Ⅰ)知, ![]() ,
,![]()
由题意可设![]() ,
,![]() .
.
因为![]()
所以![]()
由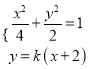 整理得:
整理得:![]()
因为![]()
所以![]() ,
,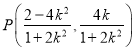
所以![]()
(Ⅲ)设![]() ,则
,则![]() .
.
若以![]() 为直径的圆恒过
为直径的圆恒过![]() ,
,![]() 的交点,则
的交点,则![]() ,
,
所以![]() 恒成立
恒成立
由(Ⅱ)可知![]() ,
,
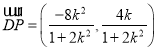 .
.
所以![]() .
.
即![]() 恒成立.
恒成立.
所以![]() .
.
所以存在![]() ,使得以
,使得以![]() 为直径的圆恒过直线
为直径的圆恒过直线![]() ,
,![]() 的交点.
的交点.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目