题目内容
在双曲线 -
- =1上求一点M,使它到左右两焦点的距离之比为3:2,并求M点到两准线的距离.
=1上求一点M,使它到左右两焦点的距离之比为3:2,并求M点到两准线的距离.
【答案】分析:设M(x1,y1),左右两焦点F1、F2,由双曲线第二定义得|MF1|=ex1+a,|MF2|=ex1-a,由已知条件得2(ex1+a)=3(ex1-a),
把e= ,a=4代入,求出点M的坐标后能得到双曲线准线方程,然后再求出点M(16,±3
,a=4代入,求出点M的坐标后能得到双曲线准线方程,然后再求出点M(16,±3 )到两条准线的距离.
)到两条准线的距离.
解答:解:设M(x1,y1),左右两焦点F1、F2,由双曲线第二定义得
|MF1|=ex1+a,|MF2|=ex1-a,
由已知2(ex1+a)=3(ex1-a),
把e= ,a=4代入,得x1=16,y1=±3
,a=4代入,得x1=16,y1=±3 .
.
∴点M的坐标为(16,±3 ).
).
双曲线准线方程为x=± =±
=± .
.
∴M(16,±3 )到准线的距离为12
)到准线的距离为12 或19
或19 .
.
点评:利用双曲线的第二定义和点到直线的距离公式求解.
把e=
 ,a=4代入,求出点M的坐标后能得到双曲线准线方程,然后再求出点M(16,±3
,a=4代入,求出点M的坐标后能得到双曲线准线方程,然后再求出点M(16,±3 )到两条准线的距离.
)到两条准线的距离.解答:解:设M(x1,y1),左右两焦点F1、F2,由双曲线第二定义得
|MF1|=ex1+a,|MF2|=ex1-a,
由已知2(ex1+a)=3(ex1-a),
把e=
 ,a=4代入,得x1=16,y1=±3
,a=4代入,得x1=16,y1=±3 .
.∴点M的坐标为(16,±3
 ).
).双曲线准线方程为x=±
 =±
=± .
.∴M(16,±3
 )到准线的距离为12
)到准线的距离为12 或19
或19 .
.点评:利用双曲线的第二定义和点到直线的距离公式求解.

练习册系列答案
相关题目
 与椭圆
与椭圆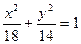 有共同的焦点,点
有共同的焦点,点 在双曲线C上.
在双曲线C上.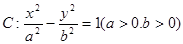 与椭圆
与椭圆 有共同的焦点,点
有共同的焦点,点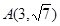 在双曲线C上.
在双曲线C上.