题目内容
17.已知函数f(x)=lnx,$g(x)=-\frac{a}{x}+\frac{3}{2}(a>0)$(1)当a=1时,若曲线y=f(x)在点M(x0,f(x0))处的切线与曲线y=g(x)在点P(x0,g(x0))处的切线平行,求实数x0的值;
(2)若?x∈(0,e],都有f(x)≥g(x),求实数a的取值范围.
分析 (1)把a=1导入解析式,并求出f′(x)和g′(x),根据切线平行对应的斜率相等列出方程,求出x0的值;
(2)根据条件设F(x)=f(x),再把条件进行转化,求出对应的解析式和导数,求出临界点,并根据导数与函数单调性的关系列出表格,再对a进行分类讨论,分别判断出函数的单调性,再求出对应的最小值,列出不等式求出a的范围.
解答 解:(1)把a=1代入得,g(x)=-$\frac{1}{x}$+$\frac{3}{2}$,
则f′(x)=$\frac{1}{x}$,g′(x)=$\frac{1}{{x}^{2}}$,
∵f(x)在点M (x0,f(x0))处的切线与
g(x)在点P (x0,g(x0))处的切线平行,
∴$\frac{1}{{x}_{0}}$=$\frac{1}{{{x}_{0}}^{2}}$,解得x0=1,
∴x0=1,
(2)由题意设F(x)=f(x)-g(x)=lnx+$\frac{a}{x}$-$\frac{3}{2}$,
∵?x∈(0,e],都有f(x)≥g(x),
∴只要F(x)在(0,e]上的最小值大于等于0即可,
则F′(x)=$\frac{1}{x}$-$\frac{a}{{x}^{2}}$=$\frac{x-a}{{x}^{2}}$,由F′(x)=0得,x=a,
F(x)、F′(x)随x的变化情况如下表:
| x | (0,a) | a | (a,+∞) |
| F′(x) | - | 0 | + |
| F(x) | 递减 | 极大值 | 递增 |
∴F(e)=1+$\frac{a}{e}$-$\frac{3}{2}$≥0,得a$≤\frac{e}{2}$,∴a≥e
当a<e时,函数F(x)在(0,a)上单调递减,在(a,e)上单调递增,
则F(a)为最小值,所以F(a)=lna+$\frac{a}{a}$-$\frac{3}{2}$,得a≥$\sqrt{e}$
∴$\sqrt{e}$≤a<e,
综上所述,a≥$\sqrt{e}$.
点评 本题考查了导数的几何意义,导数与函数单调性的关系,以及恒成立问题的转化,分类讨论思想,考查了分析问题和解决问题的能力.

练习册系列答案
相关题目
6.在三棱锥P-ABC中,PA⊥底面ABC,BC⊥AC,∠ABC=30°,AC=1,PB=2$\sqrt{3}$,则PC与平面PAB所成余弦值是( )
| A. | $\frac{\sqrt{33}}{6}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{6}$ | D. | $\frac{\sqrt{6}}{3}$ |
7.在正四面体ABCD中,平面ABC内动点P满足其到平面BCD距离与到A点距离相等,则动点P的轨迹是( )
| A. | 圆 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |
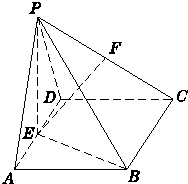 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD是等边三角形,底面ABCD是边长为2的菱形,∠BAD=60°,E是AD的中点,F是PC的中点.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD是等边三角形,底面ABCD是边长为2的菱形,∠BAD=60°,E是AD的中点,F是PC的中点.