题目内容
若连续函数 在
在 上可导,其导函数为
上可导,其导函数为 ,且函数
,且函数 的图像如图所示,则下列结论中一定成立的是( )
的图像如图所示,则下列结论中一定成立的是( )
A. 有极大值 有极大值 和极小值 和极小值 | B. 有极大值 有极大值 和极小值 和极小值 |
C. 有极大值 有极大值 和极小值 和极小值 | D. 有极大值 有极大值 和极小值 和极小值 |
D
解析试题分析:依题可得,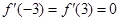 ,且当
,且当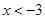 时,由
时,由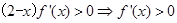 ,当
,当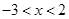 时,由
时,由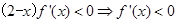 ,所以
,所以 在
在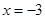 取得极大值;当
取得极大值;当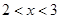 时,由
时,由 ,当
,当 时,由
时,由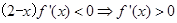 ,所以
,所以 在
在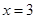 取得极小值,故选答案D.
取得极小值,故选答案D.
考点:1.函数的图像;2.极值的概念.

练习册系列答案
相关题目
如图,点 从点
从点 出发,分别按逆时针方向沿周长均为12的正三角形、正方形运动一周,
出发,分别按逆时针方向沿周长均为12的正三角形、正方形运动一周, 两点连线的距离
两点连线的距离 与点P走过的路程
与点P走过的路程 的函数关系分别记为,定义函数
的函数关系分别记为,定义函数 对于函数
对于函数 ,下列结论正确的个数是( )
,下列结论正确的个数是( )
① .
.
②函数 的图象关于直线
的图象关于直线 对称.
对称.
③函数 值域为
值域为 .
.
④函数 增区间为
增区间为 .
.
| A.1 | B.2 | C.3 | D.4 |
已知函数 ,若
,若 恒成立,则实数a的取值范围是( )
恒成立,则实数a的取值范围是( )
A. | B. |
C.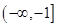 | D. |
函数 的零点所在的区间是( )
的零点所在的区间是( )
A.(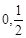 ) ) | B.( ) ) | C.( ) ) | D.( ) ) |
下列函数在区间 是增函数的是
是增函数的是
A. | B. | C. | D. |
已知偶函数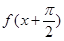 ,当
,当 时,
时, ,设
,设

 ,则( )
,则( )
A.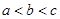 | B. | C. | D. |
下列函数中,在区间(0,+∞)上为增函数的是 ( ).
| A.y=lg(x+2) | B.y=- |
C.y= x x | D.y=x+ |
定义在R上的奇函数f(x),当x≥0时,f(x)= 则关于x的函数F(x)=f(x)-a(0<a<1)的所有零点之和为( ).
则关于x的函数F(x)=f(x)-a(0<a<1)的所有零点之和为( ).
| A.1-2a | B.2a-1 |
| C.1-2-a | D.2-a-1 |
若奇函数f(x)在(0,+∞)上的解析式是f(x)=x(1-x),则在(-∞,0)上,f(x)的解析式是( ).
| A.f(x)=-x(1-x) | B.f(x)=x(1+x) |
| C.f(x)=-x(1+x) | D.f(x)=x(1-x) |