题目内容
已知函数
，若
恒成立，则实数a的取值范围是( )
A． | B． |
C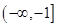． | D． |
B
解析试题分析：首先画出
的图像，
的图像为过
的一组直线，若
恒成立，只需始终在的下方，即直线夹在与
相切的直线，和
之间，所以转化为求切线斜率，=
联立，得：
①，令
，即
，解得
或
将代入①得
成立，将代入①得
，不满足
，所以舍去，或通过选项也可知道.
考点：1.函数图像的应用；2.切线斜率的求法.
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
函数
的反函数是（ ）
A． ． | B． ． |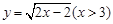
C． ． | D． ． |
函数
的定义域为（ ）
A． | B． |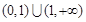
C． | D． |
若连续函数
在
上可导，其导函数为
，且函数
的图像如图所示，则下列结论中一定成立的是（ ）
A．有极大值 和极小值 | B．有极大值 和极小值 |
| C．有极大值和极小值 | D．有极大值和极小值 |
设函数
，若
和
是函数
的两个零点，
和
是的两个极值 点，则
等于( )
| A． | B． | C． | D． |
下列函数中,与函数
相同的是（ ）
A． | B． | C． | D． |
已知函数
在
时取得最大值，在
时取得最小值，则实数
的取值范围是（ ）
A． | B． | C． | D． |
为了得到函数
的图象，可以把函数
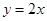的图象上所有的点（ ）
| A．向右平行移动2个单位长度 |
B．向右平行移动 个单位长度 |
| C．向左平行移动2个单位长度 |
| D．向左平行移动个单位长度 |
已知函数y＝f(x)是定义在R上的奇函数，且当x<0时，不等式f(x)＋xf′(x)<0成立，若a＝30.3f(30.3)，b＝logπ3f(logπ3)，c＝log3
f
，则a，b，c间的大小关系是( )．
| A．a>b>c | B．c>b>a |
| C．c>a>b | D．a>c>b |