题目内容
2.已知H是△ABC的垂心,B=60°,若$\overrightarrow{BH}•\overrightarrow{BC}$=6,则AC的最小值为$2\sqrt{3}$.分析 由题意画出图形,可得$|\overrightarrow{AB}|=2|\overrightarrow{BD}|$,展开数量积$\overrightarrow{BH}•\overrightarrow{BC}$,结合向量在向量方向上的投影得到ac=12.运用余弦定理后再利用基本不等式求最值.
解答  解:如图,∵H是△ABC的垂心,且B=60°,
解:如图,∵H是△ABC的垂心,且B=60°,
∴$|\overrightarrow{AB}|=2|\overrightarrow{BD}|$
∴$\overrightarrow{BH}•\overrightarrow{BC}$=$|\overrightarrow{BH}||\overrightarrow{BC}|cos∠CBH$
=$|\overrightarrow{BD}||\overrightarrow{BC}|$=$\frac{1}{2}|\overrightarrow{AB}||\overrightarrow{BC}|=\frac{1}{2}ac=6$,
∴ac=12.
则b2=a2+c2-ac≥2ac-ac=ac=12,
∴bmin=2$\sqrt{3}$,
即AC的最小值为2$\sqrt{3}$.
故答案为:$2\sqrt{3}$.
点评 本题考查平面向量的数量积运算,关键是转化思想方法的运用,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.若△ABC的面积为64,边AB与AC的等比中项为12,则sinA=( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{8}{9}$ |
17.等差数列{an}的前n项和为Sn,a7,a14,S7三数成等比数列,则其公比为( )
| A. | 2 | B. | 2或-5 | C. | 3 | D. | 3或-5 |
3.已知双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{3}$=1(a>0)过点(-2,0),则双曲线的离心率为( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{7}}{2}$ |
4.已知抛物线x2=2py的准线方程为y=-$\frac{1}{4}$,函数f(x)=sinωx的周期为4,则抛物线与函数f(x)在第一象限所围成的封闭图形的面积为( )
| A. | $\frac{6-π}{3π}$ | B. | 1 | C. | $\frac{π}{2}$ | D. | $\frac{4-π}{2π}$ |
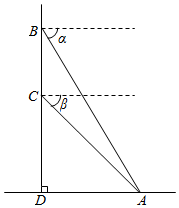 如图,山顶上有一座电视塔,在塔顶B处测得地面上一点A的俯角α=60°,在塔底C处测得点A的俯角β=45°,已知塔高60m,则山高为30($\sqrt{3}$+1).
如图,山顶上有一座电视塔,在塔顶B处测得地面上一点A的俯角α=60°,在塔底C处测得点A的俯角β=45°,已知塔高60m,则山高为30($\sqrt{3}$+1).