题目内容
（1）已知集合A={x|x2-x-6＜0}，B={x|x2+2x-8＞0}，求A∩B．
（2）当k取什么值时，一元二次不等式2kx2+kx-
＜0对一切实数x都成立？
（2）当k取什么值时，一元二次不等式2kx2+kx-
| 3 |
| 8 |
考点：一元二次不等式的解法,交集及其运算
专题：不等式的解法及应用
分析：（1）利用一元二次不等式的解法分别化简集合A，B，再利用集合的运算即可得出；
（2）当k＜0且△=k2-4×2k×(-
)＜0时满足条件，解得即可．
（2）当k＜0且△=k2-4×2k×(-
| 3 |
| 8 |
解答：
解：（1）由x2-x-6＜0，化为（x-3）（x+2）＜0，解得-2＜x＜3，∴A=（-2，3），
由x2+2x-8＞0化为（x+4）（x-2）＞0，解得x＞2或x＜-4，∴B=（-∞，-4）∪（2，+∞）．
∴A∩B=（2，3）．
（2）当k＜0且△=k2-4×2k×(-
)＜0时，解得-3＜k＜0．
即k∈（-3，0）时，一元二次不等式2kx2+kx-
＜0对一切实数x都成立．
由x2+2x-8＞0化为（x+4）（x-2）＞0，解得x＞2或x＜-4，∴B=（-∞，-4）∪（2，+∞）．
∴A∩B=（2，3）．
（2）当k＜0且△=k2-4×2k×(-
| 3 |
| 8 |
即k∈（-3，0）时，一元二次不等式2kx2+kx-
| 3 |
| 8 |
点评：本题考查了一元二次不等式的解法和集合的运算，属于中档题．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
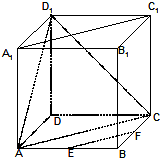如图，棱长为2的正方体ABCD-A1B1C1D1中，点E，F分别为棱AB，BC的中点．