题目内容
对于空间任意一点O和不共线的三点A、B、C,有A.必要不充分条件 B.充分不必要条件
C.充要条件 D.既不充分也不必要条件
答案:C
解析:由P、A、B、C共面![]()
![]() =
=![]() +m·
+m·![]() +n·
+n·![]()
![]()
![]() =
=![]() +m(
+m(![]() -
-![]() )+n(
)+n(![]() -
-![]() )=(1-m-n)
)=(1-m-n) ![]() +m
+m![]() +n
+n![]() ,
,
∴
反之,若x+y+z=1,则x=1-y-z,代入已知条件,得![]() =(1-y-z)
=(1-y-z) ![]() +y
+y![]() +z
+z![]() .
.
于是![]() -
-![]() =y(
=y(![]() -
-![]() )+2(
)+2(![]() -
-![]() ),即
),即![]() =y
=y![]() +z
+z![]() .
.
由共面向量定理知P、A、B、C四点共面.故选C.

练习册系列答案
相关题目
对于空间任意一点O和不共线三点A,B,C,点P满足
=x
+y
+z
是点P,A,B,C共面的( )
| OP |
| OA |
| OB |
| OC |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
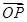 =x
=x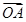 +y
+y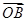 +z
+z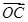 (x、y、z∈R),
(x、y、z∈R),