题目内容
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数)。在以坐标原点为极点,
为参数)。在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 。
。
(1)写出曲线![]() ,
,![]() 的普通方程;
的普通方程;
(2)过曲线![]() 的左焦点且倾斜角为
的左焦点且倾斜角为![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() 两点,求
两点,求![]() 。
。
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】分析:(1)将曲线![]() 中的参数消去可得曲线
中的参数消去可得曲线![]() 的普通方程,根据极坐标与直角坐标间的变换公式消去
的普通方程,根据极坐标与直角坐标间的变换公式消去![]() 中的
中的![]() 可得
可得![]() 的直角坐标方程.(2)由条件求出直线
的直角坐标方程.(2)由条件求出直线![]() 的参数方程为
的参数方程为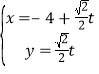 (
(![]() 为参数),将其代入曲线
为参数),将其代入曲线![]() 的普通方程后根据参数
的普通方程后根据参数![]() 的几何意义求解.
的几何意义求解.
详解:(1)将参数方程![]() (
(![]() 为参数)中的参数
为参数)中的参数![]() 消去,
消去,
得![]() ,
,
即![]() ,
,
∴曲线![]() 的普通方程为
的普通方程为![]() .
.
将![]() ,
,![]() ,
,![]() 代入
代入![]() ,
,
得![]() ,
,
∴曲线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(2)由题意知曲线![]() 左焦点为
左焦点为![]() ,直线
,直线![]() 的倾斜角为
的倾斜角为![]() ,
,
∴直线![]() 的参数方程为
的参数方程为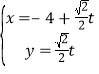 (
(![]() 为参数),
为参数),
将直线![]() 的参数方程代入
的参数方程代入![]() 整理可得
整理可得
![]() ,
,
其中![]() .
.
设点![]() 对应的参数分别为
对应的参数分别为![]() ,
,
则![]() ,
,![]() .
.
∴![]() .
.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
【题目】某校为了解高一新生对文理科的选择,对1 000名高一新生发放文理科选择调查表,统计知,有600名学生选择理科,400名学生选择文科.分别从选择理科和文科的学生随机各抽取20名学生的数学成绩得如下累计表:
分数段 | 理科人数 | 文科人数 |
|
| |
|
| |
|
|
|
| 正 | 正 |
| 正 |
|
|
|
|
(1)从统计表分析,比较选择文理科学生的数学平均分及学生选择文理科的情况,并绘制理科数学成绩的频率分布直方图.

(2)根据你绘制的频率分布直方图,估计意向选择理科的学生的数学成绩的中位数与平均分.

