题目内容
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,∠BCD=135°,侧面PAB⊥底面ABCD,∠BAP=90°,AB=AC=PA=2,E,F分别为BC,AD的中点,点M在线段PD上.

(Ⅰ)求证:EF⊥平面PAC;
(Ⅱ)若M为PD的中点,求证:ME∥平面PAB;
(Ⅲ)如果直线ME与平面PBC所成的角和直线ME与平面ABCD所成的角相等,求![]() 的值.
的值.
【答案】(Ⅰ)见解析;(Ⅱ)见解析;(Ⅲ)![]()
【解析】
试题分析:![]() 由平行四边形的性质可得
由平行四边形的性质可得![]() ,即
,即![]() ,由面面垂直的性质得出
,由面面垂直的性质得出![]() 平面
平面![]() ,故
,故![]() ,从而
,从而![]() 平面
平面![]()
![]() 以
以![]() 为原点建立空间直角坐标系,设
为原点建立空间直角坐标系,设![]() ,
,![]() ,求出平面
,求出平面![]() ,平面
,平面![]() 的法向量
的法向量![]() 以及
以及![]() 的坐标,根据线面角相等列方程求解即可得到答案
的坐标,根据线面角相等列方程求解即可得到答案
解析:(1)证明:在平行四边形![]() 中,因为
中,因为![]() ,
,![]() ,
,
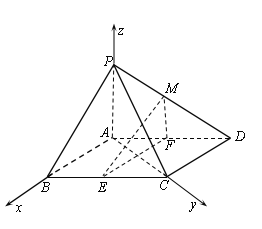
所以![]() .由
.由![]() 分别为
分别为![]() 的中点,得
的中点,得![]() , 所以
, 所以![]() .
.
因为侧面![]() 底面
底面![]() ,且
,且![]() ,所以
,所以![]() 底面
底面![]() .
.
又因为![]() 底面
底面![]() ,所以
,所以![]() .
.
又因为![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)解:因为![]() 底面
底面![]() ,
,![]() ,所以
,所以![]() 两两
两两
垂直,以![]() 分别为
分别为![]() 、
、![]() 、
、![]() ,建立空间直角坐标系,则
,建立空间直角坐标系,则
![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,
所以![]() ,
,![]() ,易得平面
,易得平面
![]() 的法向量
的法向量![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,由
,由![]() ,
,![]() ,得
,得![]() 令
令![]() , 得
, 得![]() .
.
因为直线![]() 与平面
与平面![]() 所成的角和此直线与平面
所成的角和此直线与平面![]() 所成的角相等,
所成的角相等,
所以![]() ,即
,即![]() ,所以
,所以 ![]() ,
,
解得![]() ,或
,或![]() (舍). 综上所得:
(舍). 综上所得:![]()

【题目】某社区为了解居民参加体育锻炼的情况,从该社区随机抽取了18名男性居民和12名女性居民,对他们参加体育锻炼的情况进行问卷调查.现按是否参加体育锻炼将居民分成两类:甲类(不参加体育锻炼)、乙类(参加体育锻炼),结果如下表:
甲类 | 乙类 | |
男性居民 | 3 | 15 |
女性居民 | 6 | 6 |
(Ⅰ)根据上表中的统计数据,完成下面的![]() 列联表;
列联表;
男性居民 | 女性居民 | 总计 | |
不参加体育锻炼 | |||
参加体育锻炼 | |||
总计 |
(Ⅱ)通过计算判断是否有90%的把握认为参加体育锻炼与否与性别有关?
附: ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.01 |
| 2.706 | 3.841 | 6.635 |