题目内容
20．两圆x2+y2=9和x2+y2-8x+6y+9=0的公切线条数是（ ）| A． | 1条 | B． | 2条 | C． | 3条 | D． | 4条 |
分析 把两圆的方程化为标准形式，求出圆心和半径，根据两圆的圆心距小于半径之和，可得两圆相交，由此可得两圆的公切线的条数．
解答 解：圆x2+y2=9表示以（0，0）为圆心，半径等于3的圆．
圆x2+y2-8x+6y+9=0即 （x-4）2+（y+3）2=16，表示以（4，-3）为圆心，半径等于4的圆．
两圆的圆心距等于$\sqrt{{4}^{2}+{3}^{2}}$=5，小于半径之和，大于半径差，故两圆相交，故两圆的公切线的条数为2，
故选B．
点评 本题主要考查圆的标准方程的特征，两圆的位置关系的确定方法，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
10．已知α，β为不重合的两个平面，直线m?α，那么“m⊥β”是“α⊥β”的（ ）
| A． | 充分而不必要条件 | B． | 必要而不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
15．在某次商品促销活动中，某人可得到4件不同的奖品，这些奖品要从40件不同的奖品中随机抽取决定，用系统抽样的方法确定这个人所得到的4件奖品的编号，有可能的是（ ）
| A． | 3，9，15，11 | B． | 3，12，21，40 | C． | 8，20，32，40 | D． | 2，12，22，32 |
5．
已知斜三棱柱ABC-A1B1C1的底面是边长为4的正三角形，侧棱长为5，点D，E，F分别是BB1，AA1，CC1，的中点，若侧棱AA1与底面三角形的相邻两边都成60°角，则四棱锥D-A1C1EF的体积是（ ）
已知斜三棱柱ABC-A1B1C1的底面是边长为4的正三角形，侧棱长为5，点D，E，F分别是BB1，AA1，CC1，的中点，若侧棱AA1与底面三角形的相邻两边都成60°角，则四棱锥D-A1C1EF的体积是（ ）| A． | $\frac{{20\sqrt{2}}}{3}$ | B． | $\frac{{20\sqrt{3}}}{3}$ | C． | $\frac{{50\sqrt{2}}}{9}$ | D． | $\frac{{50\sqrt{3}}}{9}$ |
12．已知f（x）=$\left\{\begin{array}{l}{（6-a）x-4a，x＜1}\\{lo{g}_{a}x，x≥1}\end{array}\right.$在区间（-∞，+∞）上是单调递增函数，则实数a的取值范围是（ ）
| A． | （1，6） | B． | [$\frac{6}{5}$，6） | C． | [1，$\frac{6}{5}$] | D． | （1，+∞） |
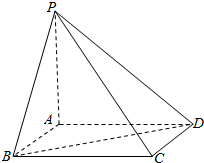在四棱锥P-ABCD中：ABCD是正方形，PA⊥平面ABCD，PA=AB=a．