题目内容
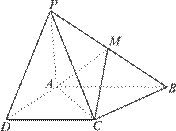
如图所示, 已知四棱锥 的底面为直角梯形,
的底面为直角梯形, 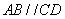 ,
, 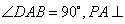 底面
底面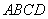 , 且
, 且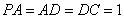 ,
, 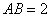 ,
,  是
是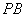 的中点.
的中点.
 (1)求证:平面
(1)求证:平面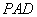
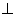 平面
平面 .
.
(2)求 与
与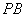 所成角的余弦值.
所成角的余弦值.
(3)求二面角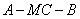 的余弦值.
的余弦值.
证明:以 为坐标原点,
为坐标原点, 长为单位长度,如图建立空间直角坐标系,则各点坐标为
长为单位长度,如图建立空间直角坐标系,则各点坐标为
 。
。
(1) ,
, ,
,
又 ,
, 平面
平面 。
。
 平面
平面 ,
, 平面
平面 平面
平面 。
。
(2) ,
, ,
,
 。
。
(3)在 上取一点
上取一点 ,则存在
,则存在 ,
,
使 ,
,
 。
。
要使 ,只需
,只需 ,即
,即
解得 。可知当
。可知当 时,点
时,点 坐标为
坐标为 ,能使
,能使 。
。
此时 ,
, ,有
,有 。
。
由 得
得 ,
, 。
。

 为所求二面角的平面角。
为所求二面角的平面角。

 。
。

练习册系列答案
相关题目
从某大学中随机抽取8名女大学生, 其身高和体重数据如表所示.
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 身高/cm | 165 | 165 | 157 | 170 | 175 | 165 | 155 | 170 |
| 体重/kg | 48 | 57 | 50 | 54 | 64 | 61 | 43 | 59 |
已知该大学某女大学生身高为165.25cm, 则预报其体重合理值为 kg.
 的渐近线方程为
的渐近线方程为 ,则
,则 的值为( )
的值为( ) 是定义域为
是定义域为 的偶函数,当
的偶函数,当 时,
时, , 若关于
, 若关于 的方程
的方程 ,
, 有且仅有6个不同实数根,则实数
有且仅有6个不同实数根,则实数 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
 的展开式中的常数项为
的展开式中的常数项为 , 则实数
, 则实数 的值为( )
的值为( )



 若
若 ,则△ABC的形状为
,则△ABC的形状为  满足条件
满足条件 ,当且仅当
,当且仅当 时,
时, 取最小值,则实数
取最小值,则实数 的取值范围是
的取值范围是 B.
B. C.
C. D.
D.
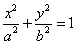 ,双曲线 C2 的方程为
,双曲线 C2 的方程为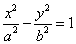 ,C1 与 C2 的离心率之积为
,C1 与 C2 的离心率之积为 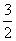 , 则 C1 、 C2 的离心率分别为
, 则 C1 、 C2 的离心率分别为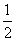 ,3 B.
,3 B.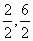 C.
C.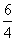 ,2 D.
,2 D.