题目内容
【题目】在某大学自主招生考试中，所有选报Ⅱ类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试，成绩分为
， 
， 
， 
， 
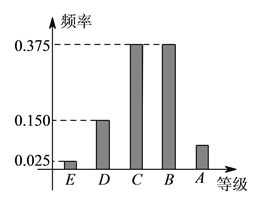
五个等级．某考场考生两科的考试成绩的数据如下图所示，其中“数学与逻辑”科目的成绩为
的考生有
人．
（Ⅰ）求该考场考生中“阅读与表达”科目中成绩为
的人数．
（Ⅱ）若等级
， 
， 
， 
， 
分别对应
分， 
分， 
分， 
分， 
分．
（ⅰ）求该考场考生“数学与逻辑”科目的平均分．
（ⅱ）若该考场共有
人得分大于
分，其中有
人
分， 
人
分， 
人
分．
从这
人中随机抽取两人，求两人成绩之和的分布列和数学期望．
科目：数学与逻辑 | 科目：阅读与表达 |
|
|
【答案】（Ⅰ）3 （Ⅱ）ⅰ：平均分为2.9 ⅱ：分布列见解析，数学期望为
【解析】试题分析：（Ⅰ）由数学与逻辑中成绩等级为B的考生有10人，频率为
，可求考场中的人数，然后结合其频率可求；（Ⅱ）ⅰ：结合频率分布直方图可求该考场考生“数学与逻辑”科目的平均分；ⅱ：设两人成绩之和为ξ，则ξ的值可以为16，17，18，19，20，然后求出ξ去每个值对应的概率，即可求解出ξ的分布列及ξ的数学期望；
试题解析：
（Ⅰ）∵“数学与逻辑”科目中等级为
的考生有
人，
∴考场共有
人，
∴“阅读与表达”科目中成绩等级为
的人数为
人．
（Ⅱ）ⅰ：平均分为
分，
ⅱ：设两个人成绩之和为
，则
的值可以为
， 
， 
， 
， 
．
， 
，
， 
，
．
∴
的分布列为
|
|
|
|
|
|
|
|
|
|
|
|
∴
，
∴
的数学期望为
．
练习册系列答案
相关题目
