题目内容

设单位向量
e1
，
e2
的夹角为60°，则向量3
e1
+4
e2
与向量
e1
的夹角的余弦值是（　　）
A、
3
4
B、
5
37
C、
25
37
D、
5
37
分析：利用向量的数量积公式求出
e1
•
e2
；利用向量的运算律求出(3
e1
+4
e2
)•
e1
；利用向量模的平方等于向量的平方求出(3
e1
+4
e2
)的模；再利用向量的数量积公式求出(3
e1
+4
e2
)与
e1
的夹角的余弦值．
解答：解：|
e1
|=1，|
e2
|=1，
e1
•
e2
=|
e1
|•|
e2
|cos60°=
1
2
，
(3
e1
+4
e2
)•
e1
=3
e1
2+4
e1
•
e2
=5，|3
e1
+4
e2
|=
(3
e1
+4
e2
)2
=
9
e1
2+24
e1
•
e2
+16
e2
2
=
37
，
cosθ=
(3
e1
+4
e2
)•
e1
|3
e1
+4
e2
|•|
e1
|
=
5
37
．
故选D
点评：本题考查向量的数量积公式并利用此公式求向量的夹角余弦、考查向量模的平方等于向量的平方并利用此性质解决与模有关的问题．
练习册系列答案
相关题目
设单位向量
e1
、
e2
夹角是60°，
a
=
e1
+
e2
，
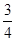b
=
e1
+t
e2
，若
a
、
b
夹角为锐角，则t的取值范围是（　　）
设单位向量
e1
、
e2
夹角是60°，
a
=
e1
+
e2
，
b
=
e1
+t
e2
若
a
、
b
夹角为锐角，则实数t的取值范围是
t＞-1 且t≠1
t＞-1 且t≠1
．
（2013•泰安二模）设单位向量
e1
，
e2
满足
e1
•
e2
=-
1
2
，则|
e1
+2
e2
|=
3
3
．

设单位向量e1、e2的夹角为60°，则向量3e1＋4e2与向量e1的夹角的余弦值是（    ）

A.            B.           C.               D.

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网