题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c,已知cos 2C=- .
.
(1)求sin C的值;
(2)当a=2,2sin A=sin C时,求b及c的长.
解 (1)∵cos 2C=1-2sin2C=- ,0<C<π,
,0<C<π,
∴sin C=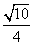 .
.
(2)当a=2,2sin A=sin C时,由正弦定理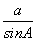 =
=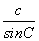 ,
,
得c=4.
由cos 2C=2cos2C-1=- 及0<C<π,
及0<C<π,
得cos C=±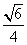 .
.
由余弦定理c2=a2+b2-2abcos C,
得b2±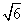 b-12=0(b>0),
b-12=0(b>0),
解得b=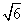 或2
或2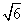 ,
,


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 C.
C.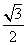 D.1
D.1 ≥a恒成立,则实数a的取值范围是( )
≥a恒成立,则实数a的取值范围是( )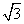 ,b=4
,b=4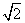 ,则B等于( )
,则B等于( )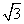 ac,则角B的值为( )
ac,则角B的值为( )
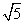 B.
B.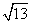
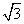 <x<2
<x<2 到直线
到直线 的距离是( )
的距离是( ) B.
B. C.
C. D.
D.