题目内容
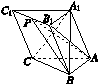
如图K459所示,在三棱柱ABC A1B1C1中,AB⊥AC,顶点A1在底面ABC上的射影恰为点B,且AB=AC=A1B=2.
(1)证明:平面A1AC⊥平面AB1B;
(2)求棱AA1与BC所成角的大小;
(3)若点P为B1C1的中点,请求出二面角P AB A1的余弦值.
图K459
解:(1)证明:∵A1B⊥平面ABC,∴A1B⊥AC,
又AB⊥AC,AB∩A1B=B,∴AC⊥平面AB1B,
∵AC⊂平面A1AC,∴平面A1AC⊥平面AB1B.
(2)以A为原点,建立如图所示的空间直角坐标系,

则C(2,0,0),B(0,2,0),A1(0,2,2),B1(0,4,2),C1(2,2,2),
 (3)∵P为棱B1C1的中点,∴易求得P(1,3,2).
(3)∵P为棱B1C1的中点,∴易求得P(1,3,2).
设平面PAB的一个法向量为n1=(x,y,z),
 得
得 令z=1,则n1=(-2,0,1),
令z=1,则n1=(-2,0,1),
而平面ABA1的一个法向量为n2=(1,0,0),
 由题可知二面角P AB A1为锐角,
由题可知二面角P AB A1为锐角,
故二面角P AB A1的余弦值是 .
.

练习册系列答案
相关题目
 点M在OA上,且OM=2MA,N为BC的中点,则
点M在OA上,且OM=2MA,N为BC的中点,则 等于( )
等于( )
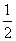 a-
a- b+
b+
 B.
B.
 D.
D.
 ,D是AC的中点.
,D是AC的中点.
 取正数时,最小值为2 的是( )
取正数时,最小值为2 的是( )




 ] 时,函数y=f(x)的最小值为
] 时,函数y=f(x)的最小值为  ,试确定常数a的值.
,试确定常数a的值. 是奇函数.
是奇函数.