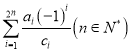题目内容
【题目】过抛物线
上一点
作直线交抛物线E于另一点N.
（1）若直线MN的斜率为1，求线段
的长.
（2）不过点M的动直线l交抛物线E于A，B两点，且以AB为直径的圆经过点M，问动直线l是否恒过定点．如果有求定点坐标，如果没有请说明理由．
【答案】（1）
（2）有，定点
．
【解析】
（1）将点
代入抛物线方程求出
，可得抛物线方程，求出直线
的方程，将直线与抛物线联立求出交点，从而利用两点间的距离公式即可求解.
（2）设出直线AB的方程：
，将直线与抛物线联立消
，利用
，可得
，设
，利用韦达定理，结合
，利用向量数量积的坐标运算整理可得
，从而可得
，代入直线方程即可求解.
（1）把代入
中，得
直线的方程：
，
即：
与
联立
得：
，
∴
，
；∴
∴．
（2）设直线AB的方程为：与联立，
得：
，
设，
，即
，
∵
，∴
∴
整理得：
代入得：
即
∴
（舍去），（符合）
∴直线
∴
即动直线AB经过定点．
练习册系列答案
名校联盟快乐课堂系列答案
相关题目
