题目内容
已知a=(解:因为f(x)=sin(x+![]() ),
),
x+![]() ∈(
∈(![]() ),
),
所以f(x)=t∈(-1,1),且在(![]() )上是严格单调递增的.
)上是严格单调递增的.
于是“方程[f(x)]2+mf(x)+n=0在区间(![]() )内有两个不等的实根”等价于“方程g(t)=t2+mt+n=0在区间(-1,1)内有两个不等的实根”.
)内有两个不等的实根”等价于“方程g(t)=t2+mt+n=0在区间(-1,1)内有两个不等的实根”.
所以“方程[f(x)]2+mf(x)+n=0在区间(![]() )内有两个不等的实根”等价于
)内有两个不等的实根”等价于
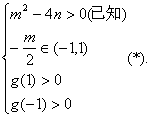
先证明充分性:由|m|+|n|<1得
|m|<1![]() <1,且1>±m-n,
<1,且1>±m-n,
即g(±1)>0.所以充分性成立.
再证不必要性:取m=1,n=![]() ,显然满足(*),但
,显然满足(*),但
是|m|→|n|<1不成立,
即得不必要性成立.
综合以上得命题成立.

练习册系列答案
相关题目
在△ABC中,已知a=8,B=60°,A=45°,则b等于( )
A、4
| ||
B、4
| ||
C、4
| ||
D、
|